Международный факторинг
Международный факторинг – вид факторинговой операции, обеспечивающий расчеты и сервисное сопровождение финансирования поставок товаров и услуг с отсрочкой платежа в условиях, когда поставщик и покупатель являются резидентами разных государств. Международный факторинг, в отличие от операций по торговому финансированию, используется для работы по долгосрочным или бессрочным внешнеэкономическим контрактам, характеризующимся регулярностью поставок и тенденцией к увеличению товарооборота. Международный факторинг осуществляется по двум моделям: однофакторной и двухфакторной.
Однофакторная модель предусматривает оказание комплекса услуг международного факторинга, при котором Фактор и компания-клиент являются резидентами одного государства. Однофакторная модель преимущественно используется при экспортных операциях.
Двухфакторная модель предусматривает разделение функций международного факторинга между двумя факторами, являющимися резидентами двух стран, которые представляют поставщик и покупатель соответственно.
Экспорт-фактор — банк или специализированная факторинговая компания, предоставляющие услуги международного факторинга поставщику-экспортеру. В функции Экспорт-фактора могут входить осуществление трансграничных расчетов по внешнеторговым контрактам, финансирование поставщика-экспортера в объеме выручки по экспортному контракту (полностью либо частично), покрытие риска неплатежа со стороны покупателя-нерезидента, а также получение выручки с покупателя-нерезидента.
Импорт-фактор — банк или специализированная факторинговая компания, предоставляющая услуги международного факторинга в стране покупателя-нерезидента. Импорт-фактор задействуется при реализации двухфакторной модели международного факторинга. В функции Импорт-фактора могут входить осуществление трансграничных расчетов по внешнеторговым контрактам, покрытие риска неплатежа со стороны покупателя-нерезидента, получение выручки с покупателя-нерезидента.
Договор международного факторинга – двусторонний договор о факторинговом обслуживании, заключаемый между резидентами одного государства. Условия договора зависят от вида торговой операции (экспорт или импорт), осуществляемой компанией-резидентом.
Внешнеторговый контракт – договор на поставку товаров либо оказание услуг, заключаемый между российской и зарубежной компанией. Копия контракта предоставляется при заключении договора международного факторинга наряду с документами, подтверждающими факт поставки (invoice). Для целей международного факторинга во внешнеторговом контракте должен быть предусмотрен порядок расчетов на условиях отсрочки платежа.
Международная факторинговая ассоциация – организация, под эгидой которой осуществляется взаимодействие Экспорт-фактора и Импорт-фактора при реализации международного факторинга по двухфакторной модели. Банк или специализированная компания в России должны являться членами одной из двух МФА – Factors Chain International и/или International Factors Group.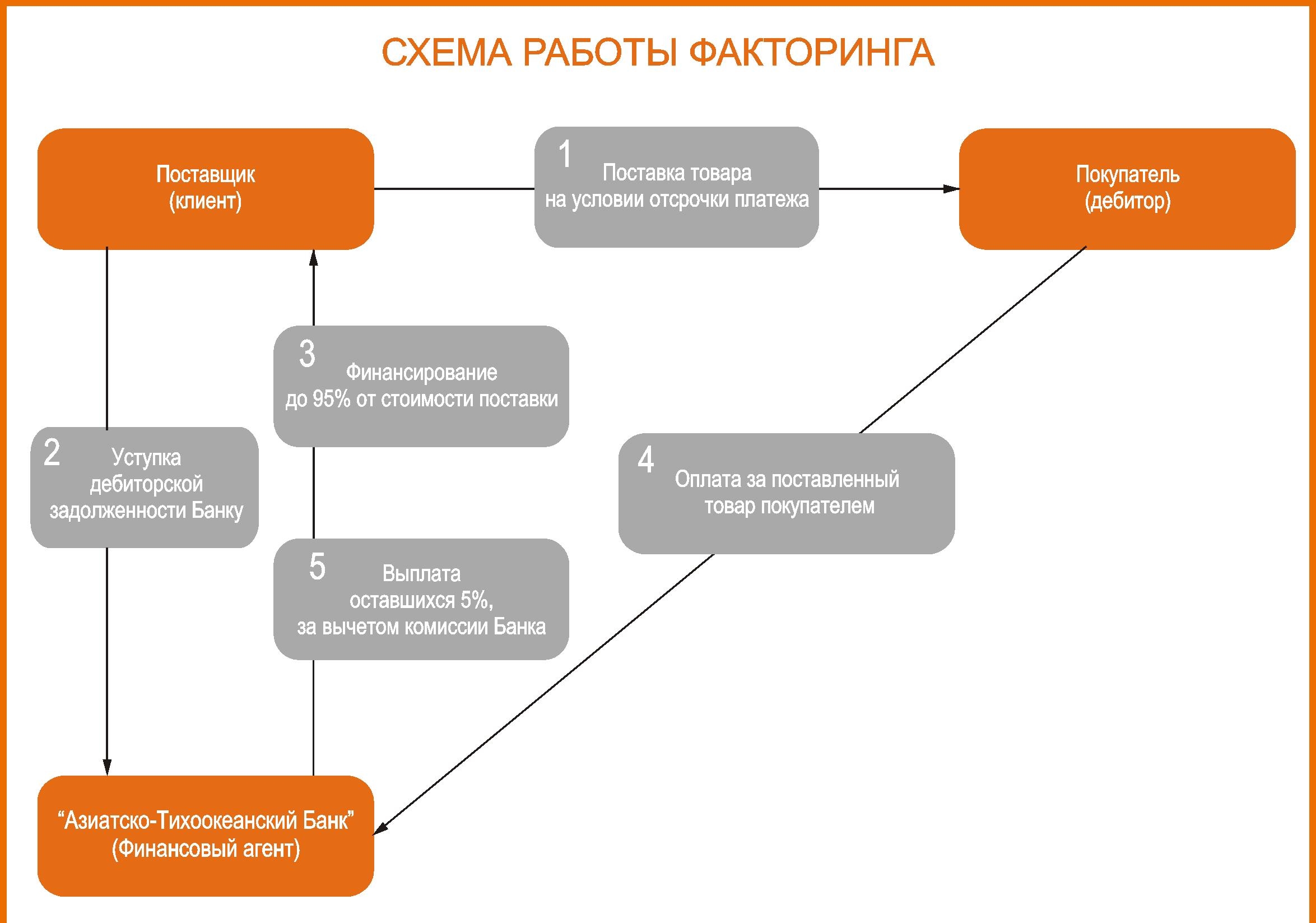
Виды международного факторинга
Документы, регулирующие международный факторинг
|
Тип поставщика |
АО, ООО или ИП |
|
Лимит финансирования |
до 500 млн ₽ |
|
Отсрочка |
до 180 дней |
|
|
открытый регрессный и безрегрессный |
|
Обеспечение |
без залога и поручительства |
|
Дебиторы |
группы компаний «Ашан», «Лента», «Леруа Мерлен», «Метро Cash&Carry», «Монетка», «О’Кей», «Тандер», X5 Retail Group, «Билла», «Гиперглобус», «Детский мир», «Дикси» |
|
Размер финансирования |
до 100% от суммы поставки |
Факторинг и дисконтирование счетов-фактур: в чем разница
Узнайте о различиях между услугами факторинга и дисконтирования счетов-фактур, позволяющими ускорить движение денежных средств по неоплаченным счетам.
Неоплаченные счета-фактуры могут серьезно нарушить потоки денежных средств вашей компании. Факторинг и дисконтирование счетов-фактур — два способа финансирования просроченной дебиторской задолженности для поддержания движения денежных средств.
Что такое факторинг счетов-фактур?
Факторинг счетов-фактур — это продажа неоплаченных счетов фактур за определенную сумму. Факторинговая компания приобретет у вас просроченные счета-фактуры за 80–90 % указанных в них сумм и берет на себя получение оплаты от дебиторов.
Так как для получения оплаты факторинговая компания имеет дело непосредственно с заказчиками, вы можете спокойно продолжать работу в обычном режиме.
Что такое дисконтирование счетов-фактур?
Дисконтирование счетов-фактур равносильно получению кредита под залог неоплаченных счетов-фактур. Дисконтная компания предоставляет вам заем на полную сумму неоплаченных счетов, который вы должны будете вернуть, когда получите оплату по счетам-фактурам.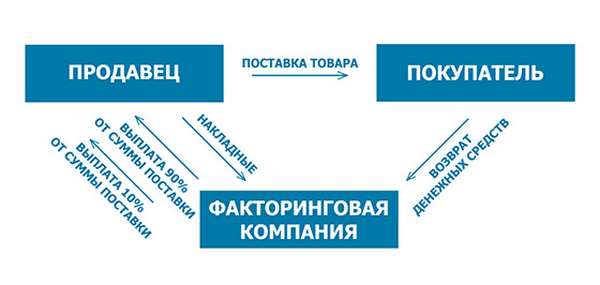
В отличие от случая с факторингом, вы получаете полную сумму, указанную в ваших просроченных счетах-фактурах, но вам придется заплатить проценты по займу. Вам также придется прикладывать усилия по сбору дебиторской задолженности, чтобы вернуть долг дисконтной компании.
Что лучше, факторинг или дисконтирование счетов-фактур?
Как правило, факторинг счетов-фактур сопровождается меньшими рисками, чем дисконтирование, но при факторинге вы получаете меньше денег за неоплаченные счета-фактуры.
Многие компании малого бизнеса предпочитают факторинг счетов просто потому, что он требует меньше усилий. Вам не нужно беспокоиться о выбивании долгов; вы можете получить большую часть суммы просроченных счетов-фактур.
Крупные компании с постоянными клиентскими базами и специализированными отделами по сбору задолженности обычно пользуются дисконтированием счетов-фактур. У них есть возможности по сбору задолженности и другие источники выручки, позволяющие возвращать займы, если не удается получить средства с заказчиков.
Упрощение финансирования счетов-фактур.
Независимо от того, какой метод финансирования счетов-фактур вы выберете, вам потребуется получать подписи для передачи или получения неоплаченных счетов. Одним щелчком мыши вы можете законно передать просроченные счета-фактуры с помощью универсального программного обеспечения для работы с электронными подписями, например Adobe Sign.
Узнайте о дополнительных возможностях Adobe Sign, позволяющих упростить выставление счетов в бизнесе.
Вакансии компании Совкомбанк Факторинг — работа в Москве, Краснодаре, Казани, Ростове-на-Дону
Совкомбанк Факторинг специализируется на оказании услуг факторинга и финансовой логистики, самый опытный игрок российского рынка, ведущий свою деятельность с 1999 года. С тех пор банковское Управление факторингового обслуживания, состоявшее из 6 человек, выросло до размеров и статуса Группы компаний, в которой работает более 370 сотрудников в 18 городах России и СНГ.
Мы входим в состав банковской группы «Совкомбанк». Сохраняя операционную самостоятельность и продуктовую специализацию, Совкомбанк Факторинг планирует наращивать темпы роста бизнеса и долю рынка при поддержке одного из крупнейших российских банков федерального уровня.
Совкомбанк Факторинг предлагает Клиентам решения, обеспечивающие комфорт для бизнеса: факторинг, в т.ч. в виде покупки дебиторской задолженности, финансирование закупок и производства, возмещение убытков от неоплат по поставкам с отсрочкой платежа. Полную информацию о факторинге и финансовой логистике Вы можете найти на первом профессиональном блоге – www.factoring.ru/blog/ Кроме того, у нас есть официальна страничка на Facebook — www.facebook.com/russianfactoring — присоединяйтесь, мы открыты к общению.
Почему Совкомбанк Факторинг?
- Работа в Совкомбанк Факторинг — это возможность приобрести уникальный опыт работы в новейшей финансовой отрасли в компании, являющейся ее родоначальником в России.

- Мы предоставляем сотрудникам большие возможности для развития: внутренние и внешние тренинги, семинары, вебинары по профессиональной тематике, обучение навыкам руководства и личной эффективности, посещение тематических конференций, стажировки в подразделениях Компании.
- Мы приветствуем горизонтальный и вертикальный рост сотрудников — большинство руководителей некогда пришли в компанию на позиции специалистов.
- Мы ценим наших сотрудников, создавая им максимально комфортные условия для работы и заботимся о том, чтобы их заработные платы соответствовали рыночным значениям.
- Мы предоставляем конкурентоспособный соцпакет: оплату ДМС, оплату ГСМ и мобильной связи по служебной необходимости, подарки детям сотрудников к Новому году и корпоративные мероприятия для всех сотрудников.
- Мы помогаем нашим сотрудникам в сложных ситуациях, предоставляя им материальную помощь по особым случаям.

- Корпоративная культура Совкомбанк Факторинг — это культура ответственности за результат и доброжелательности, взаимоуважения и коллегиального принятия решений.
Зачем малому бизнесу сейчас нужен факторинг
Пандемия изменила рынок факторинга. Если раньше для малого и среднего бизнеса факторинг (обмен будущей выручки поставщика, поставившего товар на условиях отсрочки или рассрочки платежей, на деньги) был возможен только при работе с крупными федеральными сетями, то сейчас с его помощью поставщики могут взаимодействовать с любыми сетями, интернет-магазинами и другими предприятиями. В пандемию наиболее высокие темпы роста на рынке факторинга показали производители продуктов питания, товаров первой необходимости, лекарств, медтехники и средств защиты.
Кому сегодня может быть полезен факторинг и почему есть смысл его использовать? Если ваши покупатели – торговые сети, интернет-магазины, крупные заводы, предприятия со стабильным оборотом, которые используют отсрочку, и вы поставляете им товар регулярно, можно смело использовать факторинг. Он поможет поддерживать оборотный капитал и не прибегать к классическим кредитам.
Он поможет поддерживать оборотный капитал и не прибегать к классическим кредитам.
Известно, что факторинг помогает поставщикам крупных сетей решить проблемы отсрочек платежей. Но в кризис многие магазины были вынуждены закрыться, и актуальность онлайн-торговли стало трудно переоценить. В первом полугодии 2020 г. доля онлайн-покупок в рознице выросла с 6 почти до 11% (по данным Ассоциации компаний интернет-торговли). По разным оценкам, до конца года доля онлайна в российской розничной торговле возрастет на 22%.
Однако малому бизнесу сложно самостоятельно пробиться к конечному потребителю, поэтому он сотрудничает с крупными площадками, чтобы получить готовую инфраструктуру и каналы продаж. Крупные интернет-магазины (Ozon, Wildberries, Goods, Beru и др.) диктуют свои правила ценообразования и оплаты, ставя поставщиков перед выбором: либо увеличение отсрочек платежей, либо сокращение поставок. Эту проблему может решить факторинг: поставив товар, поставщик не ждал бы два месяца, пока покупатель его оплатит, а получил бы от фактора деньги, на которые можно закупать новый товар или развивать бизнес.
Однако многие маркетплейсы не покупают товар у поставщиков, а оказывают в основном информационное сопровождение, являясь, по сути, витриной. Товар хоть и находится на складе у маркетплейса, но право собственности на него не передается, а значит, не возникает дебиторской задолженности и, следовательно, оснований для факторинга. В этом случае поставщикам подойдет специальный кредитный продукт – целевой кредит, который позволит поставщикам финансировать работу с онлайн-платформами.
Сегодня подать заявку на финансирование можно онлайн, лично документы в банк привозить не требуется. Все общение между банком, клиентом и дебитором осуществляется посредством электронного документооборота, договор подписывается электронной цифровой подписью. Банк анализирует отчетность поставщика и дебитора, заключает с поставщиком договор факторинга и предлагает дебитору подписать уведомление о факторинге. После поставки товара компания посылает банку документы, подтверждающие отгрузку, и прямо в день поставки товара получает деньги – до 90% от стоимости отгрузки. Когда покупатель оплачивает товар, банк погашает задолженность по факторингу, проценты и возвращает поставщику оставшуюся сумму.
Когда покупатель оплачивает товар, банк погашает задолженность по факторингу, проценты и возвращает поставщику оставшуюся сумму.
Следствием роста числа игроков на рынке факторинга и развития онлайн-технологий стало то, что количество факторинговых компаний или специализированных подразделений в банках значительно увеличилось. В итоге бизнес может существенно экономить. Например, если год назад в среднем ставки на факторинг составляли 15–16%, то сегодня они снизились до 11–12% годовых, а иногда и до 8–9% годовых. Еще из плюсов можно выделить бессрочный договор, к которому могут добавляться новые дебиторы, оперативное распределение лимитов среди дебиторов, отсутствие залога, так как права требования по оплате фактически передаются в залог.
Факторинг все активнее используется в госзакупках. Госкомпании и бюджетные организации должны размещать у подрядчиков из малого и среднего бизнеса не менее 15% заказов, срок расчета за выполненную поставку – 30 дней. Длительные отсрочки и долгая оплата по контракту всегда были головной болью для подрядчиков госкомпаний. Но бизнесу деньги нужны сразу – оплачивать счета, зарплату сотрудникам, закупать необходимые для производства материалы, наконец, участвовать в новых тендерах. Ускорить процесс получения средств также поможет факторинг: подрядчик по государственному или муниципальному контракту уступает банку или факторинговой компании денежное требование к заказчику, получая взамен деньги.
Но бизнесу деньги нужны сразу – оплачивать счета, зарплату сотрудникам, закупать необходимые для производства материалы, наконец, участвовать в новых тендерах. Ускорить процесс получения средств также поможет факторинг: подрядчик по государственному или муниципальному контракту уступает банку или факторинговой компании денежное требование к заказчику, получая взамен деньги.
Факторинговую компанию или банк имеет смысл выбирать из числа хорошо зарекомендовавших себя на рынке участников, например членов Ассоциации факторинговых компаний, которая объединяет ведущих игроков рынка и следит за соблюдением своими участниками всех основных стандартов и требований.
Кроме того, обязательно обратите внимание на штрафные санкции, которые предусмотрены, например, в случае возврата товара по вине продавца и за просрочку оплаты долга дебитором – часто они бывают весьма существенными.
Открытая факторинговая платформа МСП Банка получила премию ComNews Awards 2021
Проект «Открытая факторинговая платформа МСП Банка» получил премию ComNews Awards 2021 в номинации «Лучшее цифровое решение в финансовом секторе». Проект реализован совместно с компанией «Норбит» (входит в группу «Ланит») на технологической low-code/no-code платформе Creatio от «Террасофт Россия».
Проект реализован совместно с компанией «Норбит» (входит в группу «Ланит») на технологической low-code/no-code платформе Creatio от «Террасофт Россия».
В этом году на конкурс было подано более 300 заявок. После их изучения в шорт-лист вошли 50. Критериями выбора проектов-победителей стали масштабируемость, инновационность, сложность, прозрачность, эффективность и значимость.
Создание Открытой факторинговой платформы (ОФП) – одна из задач Национального проекта по акселерации малого и среднего предпринимательства. Платформа была задумана как единое цифровое пространство для взаимодействия всех участников факторинговых сделок: поставщика, заказчика и фактора. Выполняя функции института развития, МСП Банк реализовал ОФП в первую очередь для поддержки и оказания помощи компаниям поставщиков, участвующим в закупках в рамках 44-ФЗ и 223-ФЗ.
С помощью ОФП были решены главные задачи, с которыми сталкивается поставщик при поиске финансового инструмента – факторинга: прозрачность условий, предлагаемых факторами, удаленный выбор фактора, заключение с ним договора факторинга и получение финансирования. ОФП – это три личных кабинета поставщика, фактора и заказчика (покупателя). Каждому из участников доступна функциональность, соответствующая процессу заключения факторинговой сделки и выплате финансирования. Поставщик, субъект МСП, может в одном пространстве подать заявку неограниченному количеству факторов и получить от них предложения, заключив договор факторинга, подписать с заказчиком и фактором все необходимые документы для получения финансирования. Платформа отражает всю информацию о сделках, показывает текущий статус денежных требований (поставок) в едином онлайн-пространстве и аналитику по важным бизнес-показателям.
ОФП – это три личных кабинета поставщика, фактора и заказчика (покупателя). Каждому из участников доступна функциональность, соответствующая процессу заключения факторинговой сделки и выплате финансирования. Поставщик, субъект МСП, может в одном пространстве подать заявку неограниченному количеству факторов и получить от них предложения, заключив договор факторинга, подписать с заказчиком и фактором все необходимые документы для получения финансирования. Платформа отражает всю информацию о сделках, показывает текущий статус денежных требований (поставок) в едином онлайн-пространстве и аналитику по важным бизнес-показателям.
Награду получили директор по развитию бизнеса «Норбит» Владислав Игнатенко и представители заказчика МСП Банка: руководитель направления технологий и проектов Марина Стешина и главный исполнительный директор направления развития проектов и технологий Илья Горшков.
«Наше решение уникально на текущий момент, поскольку было реализовано совместно с участниками рынка – пользователями платформы. Нам удалось вовлечь представителей трех сторон факторинговой сделки – продавца (поставщика), покупателя и представителей факторинговых компаний. В рамках совместной работы было реализовано решение, которое отвечает потребностям всех участников. Это уникальный опыт на рынке разработки факторинговых онлайн-платформ», — отметила Марина Стешина.
Нам удалось вовлечь представителей трех сторон факторинговой сделки – продавца (поставщика), покупателя и представителей факторинговых компаний. В рамках совместной работы было реализовано решение, которое отвечает потребностям всех участников. Это уникальный опыт на рынке разработки факторинговых онлайн-платформ», — отметила Марина Стешина.
«Для компании «Норбит» большая честь победить с этим проектом. Благодаря профессионализму и слаженной работе наших команд у нас все получилось. Уверен, это запуск факторинговой платформы заметно упростит доступ к факторинговому финансированию для субъектов МСП», — добавил Владислав Игнатенко.
«Поздравляю МСП Банк и нашего партнера, компанию «Норбит», с победой. Мы очень рады, что заказчик использует Creatio для создания собственных уникальных решений – факторинговая платформа стала еще одним нашим совместным проектом, наряду с системой для дистанционного кредитования и краудфандинговой платформы. Это действительно значимые разработки, которые открывают новые возможности для развития малого и среднего бизнеса в России», — сообщил Алексей Клочков, управляющий директор «Террасофт Россия».
Synerdocs и Русская факторинговая компания реализуют факторинг в электронном виде
Русская Факторинговая Компания теперь оказывает факторинговые услуги в электронном виде с помощью сервиса обмена Synerdocs. Благодаря тому что из процесса исключены бумажные документы, компания может в десятки раз ускорить получение финансирования.
Электронный факторинг – это уникальная возможность значительно упростить процесс факторинга для всех участников сделки. Благодаря движению электронных документов финансовая компания может сократить время оказания услуги до одного дня.
Владимир Кузьма, директор по продажам Русской Факторинговой Компании, комментирует:
Любая компания, оказывающая
финансовые услуги, стремится улучшать процессы и технологии взаимодействия с
заказчиками. От этого напрямую зависит не только деловая репутация, но и
позиция на рынке услуг. Разумеется, перевод факторинга на электронные документы
– это серьезный шаг к модернизации сервиса, который позволит нашим клиентам
быстрее и комфортнее получать финансирование, а значит, вкладывать новые
ресурсы в свой бизнес без отсрочек.
Для перевода документов в
электронный вид мы выбрали сервис Synerdocs. При выборе платформы мы, прежде
всего, опирались на опыт специалистов и гибкость их подходов к работе с
абонентами. В течение нескольких месяцев совместной работы мы получили идеально
работающий процесс обмена документами. Уверены, что его по достоинству оценят
наши клиенты.
Электронный факторинг с помощью сервиса обмена электронными документами Synerdocs позволяет не только снизить затраты на производство, оборот и хранение документов, но и значительно упростить все этапы факторингового обслуживания. Для самих факторинговых компаний это эффективный инструмент, понижающий стоимость и трудоемкость оказания услуг.
Подробнее о том, как Русская Факторинговая Компания осуществляет свои услуги в электронном виде, вы можете узнать на официальном сайте компании: 1factor.ru.
О компании
Русская
Факторинговая Компания – крупный и авторитетный игрок на российском рынке
финансовых услуг. С августа 2009 года Русская Факторинговая Компания является
членом российской Ассоциации Факторинговых Компаний. В сентябре 2009 года стала
полноправным членом международной факторинговой ассоциации International
Factors Group.
С августа 2009 года Русская Факторинговая Компания является
членом российской Ассоциации Факторинговых Компаний. В сентябре 2009 года стала
полноправным членом международной факторинговой ассоциации International
Factors Group.
Понимание факторинга дебиторской задолженности
Факторинг дебиторской задолженности — один из способов улучшить денежный поток компании. — Getty Images / Андрей ПоповМногие малые предприятия испытывают трудности с финансированием новых проектов, пока они ждут, пока их клиенты оплатят предыдущие счета. Факторинг дебиторской задолженности — один из самых популярных способов финансирования компаний, которые борются с ограниченным денежным потоком. Факторинг использует посредника, факторинговую компанию, чтобы выкупить ваши счета и ссудить вам деньги под них.
Как работает факторинг После того, как вы доставляете товар или услугу своему клиенту, вы отправляете ему счет. Факторинговая компания платит вам немедленно, используя счет в качестве залога. Как только клиент оплачивает счет, обычно от 30 до 90 дней, транзакция закрывается.
Факторинговая компания платит вам немедленно, используя счет в качестве залога. Как только клиент оплачивает счет, обычно от 30 до 90 дней, транзакция закрывается.
Факторинг может помочь вашей компании быстро расти и обслуживать больше клиентов. Однако, как и любой вариант финансирования, у этого метода есть свои ограничения и недостатки. Вот некоторые плюсы и минусы факторинга дебиторской задолженности, которые следует учитывать.
Плюсы факторинга дебиторской задолженностиЕсть много веских причин рассматривать факторинг как способ улучшить денежный поток вашей компании.
1. Ваш бизнес немедленно получает наличные для обеспечения условий оплаты. Причина номер один для факторизации счетов — это быстрое предоставление вашей компании наличных средств для финансирования нового проекта для клиента. Большинство условий оплаты требуют, чтобы клиент заплатил в течение 30, 60 или 90 дней, что может ограничить количество клиентов, которых вы привлекаете, пока вы ждете счетов. Благодаря факторингу у вас почти сразу же есть наличные, чтобы предоставить клиентам условия оплаты и начать новые проекты.
Благодаря факторингу у вас почти сразу же есть наличные, чтобы предоставить клиентам условия оплаты и начать новые проекты.
2. Фактор счетов-фактур может иметь практически любой бизнес. Факторинг дебиторской задолженности обычно намного проще, чем подача заявки на получение бизнес-кредита. Требования довольно просты и позволяют быстро работать с новыми клиентами. Вы можете рассмотреть вопрос о факторинге, если 1) вы управляете бизнесом, у которого есть коммерческие или государственные клиенты с хорошей кредитной историей, и 2) ваш бизнес свободен от залогового удержания или других обременений и юридических проблем.Если вы соответствуете этим критериям, вы можете рассмотреть возможность факторинга.
3. Вы можете увеличить линию по мере необходимости. Факторинг счетов — отличный вариант для компаний, которые стремятся к агрессивному росту, так как он может масштабироваться вместе с вашим бизнесом. Пока ваши клиенты имеют хорошую кредитоспособность, вы можете увеличить количество факторов, поддерживаемых вашим бизнесом.
Факторинг счетов — отличный вариант для компаний, которые стремятся к агрессивному росту.
4. Это может быть долгосрочное или краткосрочное решение. Большинство факторинговых компаний будут работать с вами над созданием плана на срок до шести месяцев, чтобы помочь финансировать ваш бизнес. Если ваш бизнес вступает в период быстрого, неожиданного роста или сталкивается с финансовыми проблемами, факторинг счетов может улучшить ваш денежный поток. Как вариант, вы можете работать с факторинговой компанией в течение нескольких лет, чтобы постепенно, но неуклонно расти.
5. Ваши счета являются вашим залогом. Большинство традиционных вариантов финансирования требуют использования в качестве залога значительных активов, таких как недвижимость или бизнес-оборудование. Факторинг использует счета-фактуры только в качестве залога, поэтому вам не придется отказываться от важных для бизнеса активов, если ваш бизнес начинает испытывать трудности.
6. Факторинг может использовать бизнес любого размера. Большинство кредиторов не решатся предложить кредитную линию предприятиям без долгой кредитной истории или агрессивной нормы прибыли.Факторинг может использоваться даже самыми небольшими предприятиями для расширения вашей деятельности.
Минусы факторинга дебиторской задолженности1. Он не решает всех ваших финансовых проблем. Традиционные ссуды и кредитные линии могут использоваться по любому количеству причин, чтобы помочь вашему бизнесу оставаться успешным, например, оплата поставщикам, покупка витрины и складирование запасов. Факторинг, с другой стороны, решает только проблему ограниченного денежного потока из-за медленно платящих клиентов.
2. Это стоит больше, чем традиционные кредитные линии. Факторинг позволяет быстро получать наличные, но обычно стоит дороже, чем традиционные финансовые решения, предлагаемые кредиторами. При факторинге ставка и преимущество используются вместе для определения вашей фактической ставки, что обычно приводит к ставке 1–4% за 30 дней.
При факторинге ставка и преимущество используются вместе для определения вашей фактической ставки, что обычно приводит к ставке 1–4% за 30 дней.
3. Финансовые компании могут связываться с вашими клиентами. Когда вы начинаете деловые отношения с факторинговой компанией, они свяжутся с вашими клиентами, чтобы сообщить им, что они управляют вашими счетами.Кроме того, факторинговая компания может также связаться с вашими клиентами, если ваши платежи просрочены, что может иметь значительное негативное влияние на вашу деловую репутацию. Кроме того, ваша компания принимает на себя все безнадежные долги, возникшие во время работы с факторинговой компанией.
Факторинг счетов-фактур может помочь вам быстро решить проблемы с денежным потоком, но затраты, время и энергия могут быть не лучшим решением для вашего бизнеса. Если вы все же решили сотрудничать с факторинговой компанией, поищите ту, которая имеет положительную репутацию в вашей отрасли и работает уже много лет.
CO— не рассматривает и не рекомендует продукты или услуги. Чтобы узнать больше о выборе лучшего бизнес-кредита и вариантов финансирования, посетите наших друзей на сайте business.com.
CO— призван вдохновить вас ведущими уважаемыми экспертами. Однако, прежде чем принимать какое-либо деловое решение, вам следует проконсультироваться со специалистом, который может проконсультировать вас в зависимости от вашей индивидуальной ситуации.
Чтобы быть в курсе всех новостей, влияющих на ваш малый бизнес, перейдите сюда, чтобы быть в курсе всех наших последних новостей и обновлений малого бизнеса.
CO — стремится помочь вам начать, вести и развивать свой малый бизнес. Узнайте больше о преимуществах членства малого бизнеса в Торговой палате США здесь.
Опубликовано 25 февраля 2019 г.
Факторинговая квадратичная система: простой случай
Purplemath
«Квадратичный» — это многочлен, который выглядит как «a x 2 + b x + c», где «a», «b» и «c» — это просто числа (и либо b, либо c, но не a, может быть равно нулю).
Для простого случая факторизации квадратичных многочленов нам нужно будет найти два числа, которые будут умножаться, чтобы равняться постоянному члену c, а также суммируются до равного b, коэффициент на линейном члене x посередине. . Почему?
Квадраты — это полиномы второй степени. Когда вы учились умножать многочлены вместе, они, вероятно, начали вас с умножения двух биномов вместе (и, вероятно, они называли этот процесс «FOILing»).
Когда вы учились умножать многочлены вместе, они, вероятно, начали вас с умножения двух биномов вместе (и, вероятно, они называли этот процесс «FOILing»).
MathHelp.com
Чтобы получить квадратичный коэффициент, у которого старший коэффициент равен 1 (без дробей), каждый из исходных биномов также должен иметь старший коэффициент, равный 1.
Рассматривая два общих бинома (используя переменную x и общие числа p и q), мы можем умножить биномы следующим образом:
( x + p) ( x + q)
x 2 + p x + q x + pq
x 2 + (p + q) x + pq
В приведенном выше примере (p + q) = b и pq = c из « x 2 + b x + c». Это умножение и упрощение объясняют, почему, чтобы разложить квадратичный множитель, нам нужно начать с нахождения двух чисел (p и q выше), которые в сумме дают равное b, где эти числа также умножаются, чтобы равняться c. Этого требует логика разложения на множители (а квадратичное разложение на множители является «отменой» исходного биномиального умножения).
Это умножение и упрощение объясняют, почему, чтобы разложить квадратичный множитель, нам нужно начать с нахождения двух чисел (p и q выше), которые в сумме дают равное b, где эти числа также умножаются, чтобы равняться c. Этого требует логика разложения на множители (а квадратичное разложение на множители является «отменой» исходного биномиального умножения).
(Кстати, я называю эту тему «квадратичное разложение на множители», где в вашем учебнике эта тема может быть названа «разложением на множители трехчленов».Но «трехчленом» является любой трехчленный многочлен, который может не быть квадратичным (то есть степенью два) многочленом. И не во всех квадратиках есть три члена. Так что заголовок раздела или главы книги в лучшем случае немного не соответствует цели. Однако не беспокойтесь о разнице; название книги означает то же, что объясняется в этом уроке.)
Вот как на практике выглядит «простой» процесс квадратичной факторизации:
Этот квадратичный коэффициент имеет старший коэффициент 1, так что это простой случай факторизации. Для начала мне нужно найти множители c = +6, которые в сумме дают b = +5. У меня есть два варианта, потому что 6 факторов как произведение 2 и 3 или как произведение 1 и 6.
Для начала мне нужно найти множители c = +6, которые в сумме дают b = +5. У меня есть два варианта, потому что 6 факторов как произведение 2 и 3 или как произведение 1 и 6.
Теперь, поскольку я умножаю на положительное шесть, тогда мои множители должны иметь одинаковый знак; они оба должны быть положительными, иначе они оба должны быть отрицательными, потому что именно так работают отрицания. Поскольку я добавляю положительную пятерку, оба фактора должны быть положительными.
Я проверю суммы пар потенциальных факторов, чтобы увидеть, какой из них работает:
Так как мне нужно, чтобы мои множители суммировались до плюс пять, я буду использовать множители +2 и +3.
Еще когда я научился умножать многочлены, я знаю, что они получили эту квадратичную, умножая два бинома. Поскольку ведущий коэффициент равен 1, я знаю, что ведущий коэффициент каждого из этих биномов также должен был быть равен 1. Это означает, что вначале продукт выглядел примерно так:
Это означает, что вначале продукт выглядел примерно так:
( x ) ( x )
В конце каждой скобки идут числа, которые умножаются на +6 и складываются до +5.Это означает, что я могу завершить факторинг, вставив эти числа в скобки в любом порядке:
Почему «в любом порядке»? Поскольку передние концы двух скобок были одинаковыми, в любом случае я бы получил одинаковую факторизацию. Помните: порядок не имеет значения при умножении.
Вот как будут работать все «легкие» квадратики: мы находим множители постоянного члена, которые складываются в средний член, а затем мы используем эти множители для заполнения скобок.
Между прочим, мы всегда можем проверить нашу работу, умножив наши множители обратно вместе, и убедиться, что мы вернулись к исходному ответу. Чтобы проверить приведенную выше факторизацию, умножение выглядит следующим образом:
Ваш текст или учитель могут ссылаться на факторинг «по группировке», который рассматривается в уроке по простому факторингу. В «легком» случае факторинга использование метода «группировки» просто дает вам дополнительную работу.Например, в приведенной выше задаче, помимо нахождения множителей +6, которые складываются с +5, вам пришлось бы выполнить следующие дополнительные шаги:
В «легком» случае факторинга использование метода «группировки» просто дает вам дополнительную работу.Например, в приведенной выше задаче, помимо нахождения множителей +6, которые складываются с +5, вам пришлось бы выполнить следующие дополнительные шаги:
x 2 + 5 x + 6
x 2 + 3 x + 2 x + 6
( x 2 + 3 x ) + (2 x + 6)
x ( x + 3) + 2 ( x + 3)
( x + 3) ( x + 2)
Вы получите тот же ответ, что и я, но (я думаю) проще сразу перейти к заполнению скобок.
Главный член равен 1, так что это простой случай факторинга. Постоянный член — 6, который можно записать как произведение 2 и 3 или 1 и 6, как в предыдущем упражнении. Но на этот раз коэффициент по среднему члену другой. Вместо +5 у меня +7.
Но на этот раз коэффициент по среднему члену другой. Вместо +5 у меня +7.
Знак у постоянного члена такой же, как и раньше (а именно «плюс»), поэтому мне все равно понадобятся множители «плюс». Но сумма (то есть среднесрочный коэффициент) другая; теперь это 7.В то время как 2 + 3 = 5 работали для предыдущего квадратичного, +2 и +3 не те числа, которые мне нужны в этом случае. С другой стороны, 1 + 6 = +7, поэтому я буду использовать +1 и +6 для факторизации. И я также сразу перейду от этого вывода к тому, чтобы записать свой окончательный ответ:
Опять же, помните, что порядок не имеет значения при умножении, поэтому приведенный выше ответ с равной точностью можно записать как «( x + 6) ( x + 1)».
Постоянный член (созданный умножением) равен +6, поэтому мои множители будут либо «плюс», либо оба «минус». Но средний коэффициент на этот раз «минус». Поскольку я добавляю к «минусу» (а именно к –5), то оба множителя должны быть «минусом».
Поскольку я добавляю к «минусу» (а именно к –5), то оба множителя должны быть «минусом».
Когда коэффициент среднего члена был «плюс» пять, я использовал множители +2 и +3. Теперь, когда коэффициент моего среднего члена равен «минус», я буду использовать –2 и –3:
Обратите внимание, что мы можем использовать подсказки по знакам, чтобы определить, какие пары факторов использовать, как я продемонстрировал в предыдущих упражнениях.Формально правила выглядят так:
- Если c равно «плюс», то оба множителя будут либо «плюс», либо оба «минус».
- Если b равно «плюс», то оба множителя равны «плюс».
- Если b равно «минус», то оба множителя равны «минус».
- В любом случае ищите множители, которые добавляют к b.
- Если c равно «минус», то множители будут иметь чередующиеся знаки; то есть один будет «плюс», а другой — «минус».

- Если b равно «плюс», то больший из двух множителей равен «плюсу».
- Если b равно «минус», то больший из двух множителей равен «минус».
- В любом случае ищите множители, которые вычитают до b; то есть коэффициенты, которые составляют b единиц , кроме .
Старший коэффициент равен 1, так что это квадратичный коэффициент простого разложения.Я умножаю на «плюс» шесть, поэтому оба множителя будут либо «плюс», либо оба «минус». Глядя на средний член, я вижу, что добавляю к «минусу» семь, поэтому оба моих множителя будут «минус».
(Отрицательные) множители +6, которые в сумме дают 7, — это –1 и –6, поэтому я буду использовать –1 и –6 для моей факторизации:
До сих пор c (постоянный член) всегда был плюсом. Что, если c — «минус»?
Поскольку я умножаю на «минус» шесть, мне нужны множители с противоположными знаками; то есть один множитель будет «плюс», а другой — «минус». Коэффициент при среднем члене равен «плюс» 1, поэтому я знаю, что больший из двух факторов (больший, то есть по абсолютной величине) получит знак «плюс». Поскольку эти числа с противоположными знаками будут сложены вместе, чтобы получить +1, мне нужно, чтобы эти два множителя были разделены на одну единицу.
Коэффициент при среднем члене равен «плюс» 1, поэтому я знаю, что больший из двух факторов (больший, то есть по абсолютной величине) получит знак «плюс». Поскольку эти числа с противоположными знаками будут сложены вместе, чтобы получить +1, мне нужно, чтобы эти два множителя были разделены на одну единицу.
Пары факторов для 6 — это 1 и 6, а также 2 и 3. Значения во второй паре разнесены на одну единицу, поэтому я знаю, что буду использовать 2 и 3.
Поскольку мне нужно получить ответ «плюс» на сумму двух множителей, мне понадобится большее из двух моих чисел, чтобы получить знак «плюс»; а именно, 3 получит знак «плюс» (поэтому 2 получит знак «минус»).Тогда моя факторизация:
Это выглядит так же, как и предыдущая квадратичная, за исключением того, что теперь средний член — «минус». Постоянным членом по-прежнему является «минус», поэтому мне по-прежнему нужны множители с противоположными знаками. А коэффициент среднего члена (кроме его знака) по-прежнему равен 1, поэтому мне по-прежнему нужны факторы, разделенные на одну единицу. Но на этот раз больший множитель получит знак «минус».
А коэффициент среднего члена (кроме его знака) по-прежнему равен 1, поэтому мне по-прежнему нужны факторы, разделенные на одну единицу. Но на этот раз больший множитель получит знак «минус».
Все остальные соображения остаются прежними.Я по-прежнему хочу, чтобы множители 6 были разделены на одну единицу, поэтому я все еще буду использовать 2 и 3. Но на этот раз знак 3 будет «минус»:
В этом квадратичном постоянный член — «минус», поэтому мне все еще нужны множители противоположных знаков.
Однако на этот раз коэффициент среднего члена (кроме его знака) равен 5, а не 1, поэтому теперь я хочу, чтобы мои два фактора были разделены на пять единиц.И поскольку коэффициент среднего члена равен «минус», больший из двух моих факторов получит знак «минус».
Пары множителей для шести — это 1 и 6, а также 2 и 3. Числа в первой паре множителей разделены на пять, поэтому я буду использовать числа 1 и 6. Я добавляю к «минусу», поэтому я дам большему из моих множителей знак «минус»; то есть, я буду использовать +1 и –6 для этой факторизации:
Числа в первой паре множителей разделены на пять, поэтому я буду использовать числа 1 и 6. Я добавляю к «минусу», поэтому я дам большему из моих множителей знак «минус»; то есть, я буду использовать +1 и –6 для этой факторизации:
Кстати, есть один частный случай факторинга квадратиков.Раньше, когда вы разлагали простые старые числа на множители, были некоторые числа, которые не учитывались, например 5 или 13. Вспомните, что эти неопровержимые числа называются «простыми» числами. Вы всегда можете умножить два целых числа, чтобы получить другое целое число, но некоторые целые числа нельзя разделить, чтобы получить два (нетривиальных) целых числа.
Точно так же есть квадраты, которые не учитываются. Вы можете умножить два бинома (без дробей), чтобы получить квадратичный (без дробей), но не все квадратичные числа можно разложить на множители, чтобы получить два (нетривиальных) бинома. Терминология для таких квадратичных (или любого не факторизуемого многочлена) также является «простой».
Терминология для таких квадратичных (или любого не факторизуемого многочлена) также является «простой».
Старший коэффициент равен 1, так что это случай простого факторинга. Поскольку постоянным членом является «минус», мне понадобится множитель «плюс» и «минус», так что, когда я умножаю их вместе, я получаю –6, но когда я их складываю, я получаю +7. Другими словами, мне понадобятся два множителя, разделенных на семь единиц, причем больший множитель получит знак «плюс».
Пары факторов для 6 — это 1 и 6, а также 2 и 3. На первый взгляд, я могу предположить, что мне следует использовать 1 и 6, но —
Один из множителей должен быть «минус», чтобы умножить и получить «минус» шесть! Попробовав первую пару факторов из 1 и 6, сумма будет одной из следующих:
(–1) + 6 = 5
1 + (–6) = –5
Хорошо; ни один из способов не сработал. Так что, может быть, мне стоит использовать другую пару факторов …? Проверяя сложение этих чисел, я получаю:
Так что, может быть, мне стоит использовать другую пару факторов …? Проверяя сложение этих чисел, я получаю:
(–2) + 3 = 1
2 + (–3) = –1
Кто-то может подумать: «Может, мне стоит по-другому делать знаки». Но единственный способ получить множители шести в сумме до семи — поставить этим множителям один и тот же знак. Но если я это сделаю, то множители не умножатся на «минус» шесть.
Другими словами, не существует пары множителей –6, которые добавляли бы к +7. А если что-то нереализуемо, то самое главное. Итак, x 2 + 7 x -6 — простой квадратичный многочлен. С технической точки зрения, это «невозможно произвести по целым числам», так называемое, потому что я не смог найти пару целых чисел, которая бы работала. Тогда мой ответ:
URL: https: // www. purplemath.com/modules/factquad.htm
purplemath.com/modules/factquad.htm
Расширенный факторинг
Вы всегда можете использовать формулу корней квадратного уравнения, чтобы найти два корня квадратного трехчлена.
Но часто можно проще найти корни с помощью факторинга.
Иногда вы даже можете использовать факторизацию, чтобы найти корни уравнения более высокого порядка, например, кубического или четвертого многочлена. Ниже мы покажем некоторые частные случаи и то, как их разложить на множители.Пример 1:
Разложите на множители трехчлен x3 + 7×2 + 10x.
Здесь x является общим для всех терминов, поэтому его можно вынести за скобки.
x3 + 7×2 + 10x = x (x2 + 7x + 10)
Нам нужно найти два числа, сумма которых равна 7 и произведение которых равно 10, чтобы разложить на множитель x2 + 7x + 10.
Цифры 2 и 5.
х2 + 7х + 10 = (х + 2) (х + 5)
Следовательно, x3 + 7×2 + 10x = x (x + 2) (x + 5).
Пример 2:
Разложите на множители трехчлен x2y2−5xy2−24y2.
Здесь y2 является общим для всех членов, поэтому его можно вынести за скобки.
x2y2−5xy2−24y2 = y2 (x2−5x − 24)
Нам нужно найти два числа, сумма которых равна −5, а произведение которых равно −24, чтобы разложить на множители x2−5x − 24.
Среди пар факторов −24 два числа, которые имеют сумму −5, — это −8 и 2.
Итак, x2−5x − 24 = (x − 8) (x + 2).
Следовательно, x2y2−5xy2−24y2 = y2 (x − 8) (x + 2).
Пример 3:
Фактор, x4 + x2−30.
Здесь есть многочлен 4-го порядка.Подставляем x2 = X, чтобы получить эквивалентный квадратный многочлен X2 + X − 30.
Нам нужно найти два числа, сумма которых равна 1 и произведение которых равно −30, чтобы разложить на множители X2 + X − 30.
Среди пар факторов −30 два числа с суммой 1 — это −5 и 6.
Итак, X2 + X − 30 = (X − 5) (X + 6).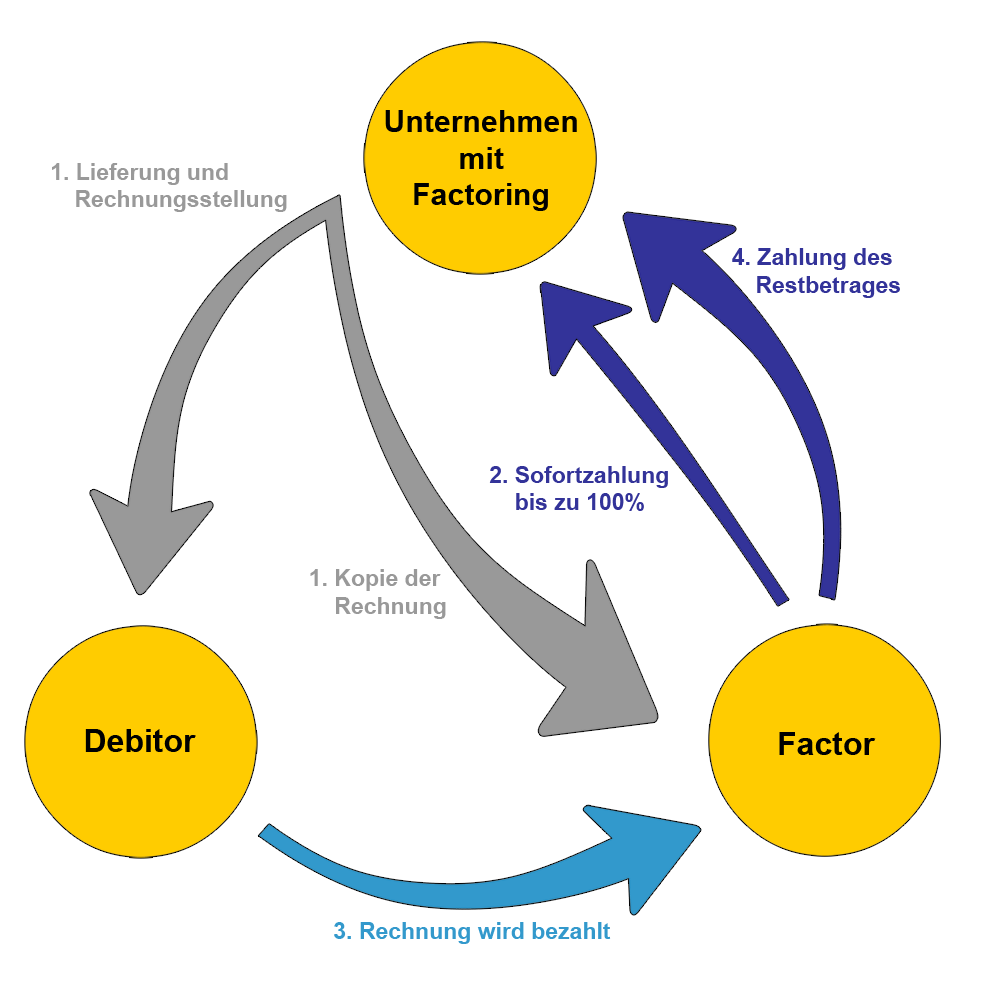
То есть x4 + x2−30 = (x2−5) (x2 + 6).
Вы можете использовать тождество a2 − b2 = (a + b) (a − b), чтобы уменьшить x2−5 как (x + 5) (x − 5).
Бином x2 + 6 неприводим; его нельзя разложить на реальные числа.
Следовательно, x4 + x2−30 = (x + 5) (x − 5) (x2 + 6).
Пример 4:
Разложите на множители многочлен x3−3×2 + 4x − 12.
Здесь ни один из вышеперечисленных способов не сработает!
Сгруппируйте первые 2 термина и последние 2 термина вместе.
x3−3×2 + 4x − 12 = (x3−3×2) + (4x − 12)
Здесь x2 является общим в первых 2 членах, а 4 — общим в последних 2 членах. Вынесите их за скобки!
(x3−3×2) + (4x − 12) = x2 (x − 3) +4 (x − 3)
Теперь вычтите множитель (x − 3).
x2 (x − 3) +4 (x − 3) = (x − 3) (x2 + 4)
Бином x2 + 4 неприводим; его нельзя разложить на реальные числа.
Следовательно, x3−3×2 + 4x − 12 = (x − 3) (x2 + 4).
Пример 5:
Разложите на множители многочлен 6×2 + 7xy + 2y2.
Нам нужно найти два числа, произведение которых равно произведению коэффициентов членов x2 и y2, а сумма равна коэффициенту среднего члена. То есть два числа, сумма которых равна 7 и произведение которых 6 умножает на 2 или 12.
Среди пар факторов, состоящих из 12, два числа с суммой 7 — это 4 и 3.
Запишите средний член трехчлена, используя числа.
6×2 + 7xy + 2y2 = 6×2 + 4xy + 3xy + 2y2
Теперь у нас есть что-то похожее на пример 4. Итак, сгруппируйте первые 2 члена и последние 2 термина вместе.
6×2 + 7xy + 2y2 = (6×2 + 4xy) + (3xy + 2y2)
Здесь 2x является общим в первых 2 членах, а y — общим в последних 2 членах. Вынесите их за скобки!
(6×2 + 4xy) + (3xy + 2y2) = 2x (3x + 2y) + y (3x + 2y)
Теперь используйте свойство распределения.
2x (3x + 2y) + y (3x + 2y) = (3x + 2y) (2x + y)
Следовательно, 6×2 + 7xy + 2y2 = (3x + 2y) (2x + y).
См. Также факторизацию по группировке и неприводимые многочлены.
Факторинг
Чтобы разложить на множители разницу между двумя квадратами, (1) найдите квадратный корень из первого члена и квадратный корень из второго члена и (2) выразите свой ответ как произведение суммы величин из шага 1 умноженная на разницу этих количеств.
Коэффициент.
Чтобы разложить на множители многочлены, имеющие три члена вида ax 2 + bx + c, (1) проверьте, можете ли вы разложить множители на множители (вычленить общие члены). Затем, если a = 1 (то есть первый член просто x 2 ), используйте двойные круглые скобки и разложите первый член на множители. Поместите эти множители в скобки слева. Например,
( x ) ( x )
(2) Разложите последний член на множители и поместите множители в правые части круглых скобок.
Чтобы определиться со знаками чисел, сделайте следующее. Если знак последнего члена отрицательный , (1) найдите два числа (одно будет положительным числом, а другое — отрицательным числом), произведение которых является последним членом, а разница составляет , коэффициент (число перед) среднего члена и (2) дают большему из этих двух чисел знак среднего члена и напротив знака для другого множителя.
Если знак последнего члена — положительный, (1) найдите два числа (оба будут положительными или оба будут отрицательными), произведение которых является последним членом, а сумма которых является коэффициентом среднего члена и (2) дайте обоим факторам знак среднего члена.
Пример 3
Фактор x 2 — 3 x — 10.
Сначала проверьте, можете ли вы мономиально множить (вычленять общие термины). Поскольку это невозможно, используйте двойные скобки и разложите первый член на множители следующим образом: ( x ) ( x ). Затем разложите последний член, 10, на 2 раза по 5 (5 должно принимать отрицательный знак, а 2 должно принимать положительный знак, потому что тогда они будут суммировать коэффициент среднего члена, который равен –3) и сложите соответствующие знаки, выезд
( x — 5) ( x + 2)
Умножение означает (внутренние члены) и крайних значений (внешние члены) для проверки.
Чтобы полностью проверить, умножьте множители вместе.
Пример 4
Фактор x 2 + 8 x + 15.
( x + 3) ( x + 5)
Обратите внимание, что 3 × 5 = 15 и 3 + 5 = 8, коэффициент среднего члена. Также обратите внимание, что знаки обоих факторов — это +, знак среднего члена. Проверить,
Пример 5
Фактор x 2 — 5 x — 14.
( x -7) ( x + 2)
Обратите внимание, что 7 × 2 = 14 и 7-2 = 5, коэффициент среднего члена. Также обратите внимание, что знак большего множителя 7 — -, а у другого множителя 2 — знак +. Проверить,
Если, однако, a ≠ 1 (то есть первый член имеет коэффициент, например, 4 x 2 +5 x + 1), тогда потребуется дополнительный метод проб и ошибок.
Пример 6
Фактор 4 x 2 +5 x + 1.
(2 x +) (2 x +) может подойти для первого семестра. Но когда единицы используются как множители для получения последнего члена (2 x + 1) (2 x + 1), средний член получается как 4 x вместо 5 x .
Поэтому попробуйте (4 x +) ( x +). Теперь использование единиц в качестве множителей для получения последних членов дает (4 x + 1) ( x + 1). Проверка на средний срок,
Следовательно, 4 x 2 + 5 x + 1 = (4 x + 1) ( x + 1).
Пример 7
Фактор 4 a 2 + 6 a + 2.
Вынос 2 листа
2 (2 а 2 + 3 а + 1)
Теперь множим как обычно, давая
2 (2 a + 1) ( a + 1)
Проверить,
Пример 8
Фактор 5 x 3 + 6 x 2 + x .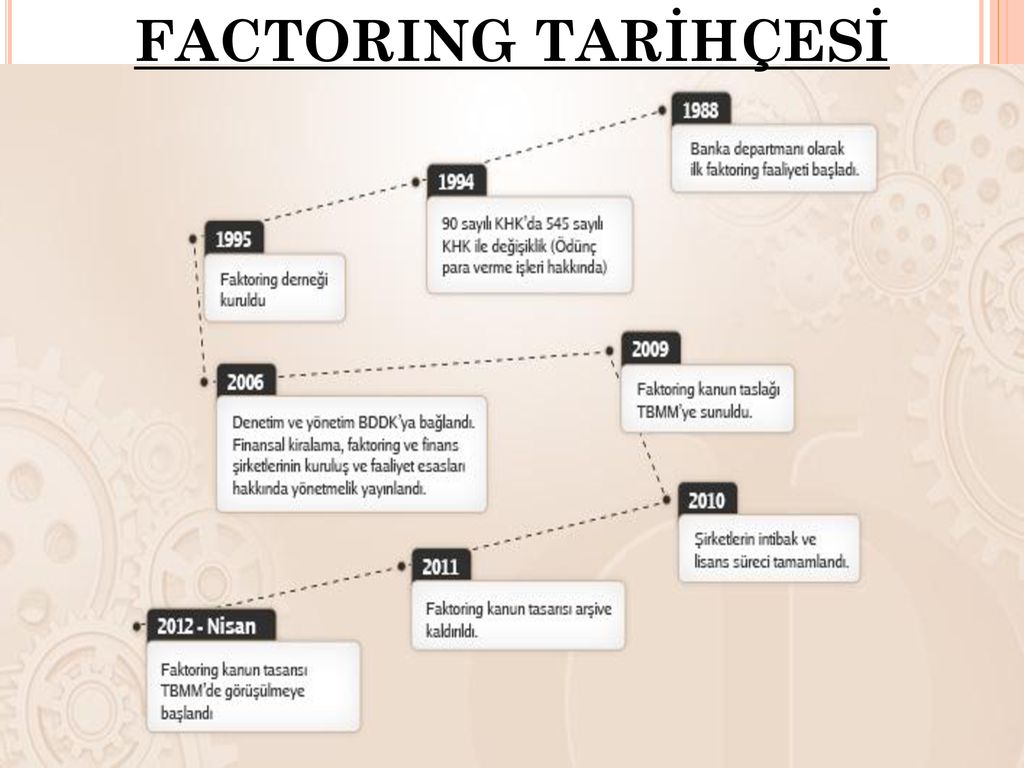
Разложение листа x
x (5 x 2 + 6 x + 1)
Теперь множим как обычно, давая
x (5 x + 1) ( x + 1)
Проверить,
Пример 9
Фактор 5 + 7 b + 2 b 2 (небольшой поворот).
(5 + 2 b ) (1 + b )
Проверить,
Обратите внимание, что (5 + b ) (1 + 2 b ) неверно, поскольку дает неправильный средний член.
Пример 10
Фактор x 2 + 2 xy + y 2 .
( x + y ) ( x + y )
Проверить,
Пример 11
Фактор 3 x 2 — 48.
Вынос 3 листа
3 ( x 2 — 16)
Но x 2 — 16 — это разница между двумя квадратами, которую можно дополнительно разложить на ( x + 4) ( x — 4). Следовательно, при полном факторинге 3 x 2 — 48 = 3 ( x + 4) ( x — 4).
Следовательно, при полном факторинге 3 x 2 — 48 = 3 ( x + 4) ( x — 4).
Факторинг по группировке
Некоторые полиномы имеют биномиальные, трехчленные и другие полиномиальные множители.
Пример 12
Фактор x + 2 + xy + 2 y .
Поскольку мономиального множителя нет, вам следует попытаться переставить члены и поискать биномиальные множители.
x + 2 + xy + 2 y = x + xy + 2 + 2 y
Группировка дает
( x + xy ) + (2 + 2 y )
Теперь факторинг дает
x (1 + y ) + 2 (1 + y )
Использование распределительного свойства дает
( x + 2) (1 + y )
Вы можете переставить их по-другому, но все равно получите тот же факторинг.
Краткое изложение методов факторинга
Факторинг многочленов следует искать в следующем порядке.
Найдите наибольший общий фактор, если он существует.
Если есть два члена, ищите разницу в квадратных числах.
Если есть три члена, ищите шаблон, который применим к ax 2 + bx + c .
Если имеется четыре или более термина, поищите какой-либо тип перегруппировки, который приведет к другому факторингу.
Примечание: Существуют многочлены, которые не могут быть факторизованы.
Пример 13
Фактор 2 x 2 + 3 x + 5.
У этого многочлена нет общего множителя.
Этот многочлен не является разностью квадратных чисел.{2} + b x + c; a \ neq 0 \)
- Шаг 1. Найдите произведение \ (a c \), то есть произведение коэффициентов при первом и последнем членах.
- Шаг 2.
 {2} +7 x + 3 \).{2} +15 х-27 \)
{2} +7 x + 3 \).{2} +15 х-27 \)- Шаг 1. Произведение \ (a c = (2) (- 27) = — 54 \)
- Шаг 2. Теперь нам нужно найти два целых числа, произведение которых равно — 54. Мы можем перечислить все возможности:
\ [(- 1) (54), \ quad (-2) (27), \ quad (-3) (18), \ quad (-6) (9), \ nonumber \]
\ [(1) (- 54), \ quad (2) (- 27), \ quad (3) (- 18), \ quad (6) (- 9) \ nonumber \]
и вычислите сумму каждой пары. Только целые числа -3 и 18 дают в сумме 15.
- Шаг 3. Мы можем переписать средний член \ (15 x = -3 x + 18 x \).{2} -11 х + 2: \)
Шаг 1. Произведение \ (a c = (12) (2) = 24 \)
Шаг 2. Нам нужно найти два целых числа, произведение которых равно 24, а сумма равна -11. Перечислим все пары множителей 24:
.\ [(1) (24), \ quad (2) (12), \ quad (3) (8), \ quad (4) (6) \ nonumber \]
\ [(- 1) (- 24), \ quad (-2) (- 12), \ quad (-3) (- 8), \ quad (-4) (- 6) \ nonumber \]
У пары -3 и -8 будет сумма -11.

Шаг 3. Перепишем средний член \ (- 11 x = (- 3 x) + (- 8 x) \).
Шаг 4.{2} -3 х-24 \):
Нам нужно найти два числа, произведение которых равно \ (a c = c = -24 \), а сумма равна -3. Число -24 можно разложить на множители:
\ [(1) (- 24), \ quad (2) (- 12), \ quad (3) (- 8), \ quad (4) (- 6) \ nonumber \]
\ [(- 1) (24), \ quad (-2) (12), \ quad (-3) (8), \ quad (-4) (6). \ Nonumber \]
Поскольку ни одна из пар в списке не дает в сумме \ (- 3 \), трехчлен нельзя разложить на множители как произведение двух биномов. Это простой многочлен.
Смешанный факторинг
Итак, мы объяснили основные методы факторизации многочленов.Вот рекомендации, которым мы можем следовать, чтобы выбрать правильный метод для полного факторизации заданного многочлена.
Рекомендации по полному разложению многочлена на множители
- Шаг 1 . Если возможно, исключите GCF из всех терминов.
- Шаг 2 .
 Подсчитайте количество членов многочлена: если многочлен состоит из двух членов, попробуйте формулу разности двух квадратов; если многочлен состоит из трех членов, попробуйте AC-метод; если многочлен состоит из четырех членов, попробуйте метод группировки.{2} -10 х + 3 \)
Подсчитайте количество членов многочлена: если многочлен состоит из двух членов, попробуйте формулу разности двух квадратов; если многочлен состоит из трех членов, попробуйте AC-метод; если многочлен состоит из четырех членов, попробуйте метод группировки.{2} -10 х + 3 \)Все, что нужно знать о лучших факторинговых компаниях — советник Forbes
Факторинговые компании, выставляющие счета-фактуры, предъявляют другие требования к участникам, авансовые ставки и факторинговые сборы, чем их конкуренты. Более того, одни факторинговые компании предлагают договоры без права регресса, тогда как другие предлагают факторинг исключительно с регрессом. При выборе факторинговой компании учитывайте следующие факторы:
Требования к финансированию
Факторинг по счетам легче квалифицировать, чем традиционные формы финансирования, но предприятия все равно должны соответствовать определенным требованиям.И поскольку факторинговая компания принимает на себя риск неплатежа, факторинговые компании также озабочены кредитоспособностью клиентов компании.

Вот некоторые общие требования, предъявляемые факторинговыми компаниями:
- Компания зарегистрирована в США.
- Компания продает предприятиям, а не напрямую потребителям
- Ежемесячные продажи не менее 5000 долларов
- Бизнес не имеет доступа к традиционному финансированию
- Клиенты платежеспособны
- У клиентов есть 30 дней или более для оплаты счетов, но не более 90 дней
Чтобы иметь право на факторинг счетов и соответствовать вышеперечисленным требованиям, факторинговые компании часто требуют, чтобы компании представляли личные и коммерческие налоговые декларации за последние три года, финансовые отчеты за период от трех до пяти лет и отчеты о сроках погашения дебиторской и кредиторской задолженности.
Предварительные ставки
Ставка аванса — это процент неоплаченных счетов, которые факторинговая компания оплачивает предприятию авансом. Процент обычно колеблется от 70% до 95%, но для большинства предприятий колеблется в районе 80%.
 Факторы, такие как стабильность бизнеса, а также отрасль бизнеса и история транзакций, обычно определяют потенциальные ставки аванса.
Факторы, такие как стабильность бизнеса, а также отрасль бизнеса и история транзакций, обычно определяют потенциальные ставки аванса.Например, строительный бизнес считается более рискованным, чем более традиционный бизнес, поэтому ставка аванса может быть ближе к 60%.Напротив, предприятия в транспортной отрасли считаются наименее рискованными, и ставки аванса могут достигать 97%.
Факторные сборы
Факторные сборы — иногда называемые дисконтными или факторинговыми ставками — это сборы, которые компании взимают с течением времени и до тех пор, пока счет не будет оплачен полностью. Эти сборы обычно варьируются от 0,50% до 5% и могут быть фиксированными или переменными. В случае фиксированных ставок факторная ставка остается неизменной до погашения счетов. При фиксированной ставке 3% с предприятия взимается ставка 3% от общей суммы счета, когда счет оплачивается, независимо от того, когда в течение срока он оплачивается.
При использовании сборов с переменным фактором ставки увеличиваются вместе с тем, как долго клиент оплачивает счет.
 Например, ставка фактора может начинаться с 1%, увеличиваться до 2% на второй неделе и до 5% на третьей неделе. В качестве альтернативы ставка может начинаться с 2% и оставаться на этом уровне в течение первых 30 дней, после этого увеличиваясь с заданными приращениями.
Например, ставка фактора может начинаться с 1%, увеличиваться до 2% на второй неделе и до 5% на третьей неделе. В качестве альтернативы ставка может начинаться с 2% и оставаться на этом уровне в течение первых 30 дней, после этого увеличиваясь с заданными приращениями.Соглашения о регрессе и без регресса
Факторинговые соглашения могут быть с правом регресса или без права регресса, что определяет, что произойдет, если счет не будет оплачен.Если компания подписывает договор факторинга с правом регресса и счет не оплачивается, предприятие должно выкупить счет или обменять его на другой счет-фактуру такой же стоимости. Соглашения о регрессе снижают риск для факторинговых компаний, выставляющих счета, и встречаются чаще, особенно в отраслях с высоким уровнем риска, таких как строительство.
В соответствии с соглашением об отказе от регресса факторинговая компания принимает на себя риск неплатежа, и компания не обязана выкупать какие-либо счета — даже те, которые не были оплачены.
 По этой причине договоры факторинга без права регресса обычно более дороги и предназначены для отраслей, которые представляют меньший риск для факторинговых компаний.
По этой причине договоры факторинга без права регресса обычно более дороги и предназначены для отраслей, которые представляют меньший риск для факторинговых компаний.Разложите многочлен или выражение на множители с помощью программы «Пошаговое решение задач по математике»
Процесс факторизации необходим для упрощения многих алгебраических выражений и является полезным инструментом при решении уравнений более высокой степени. Фактически, процесс факторизации настолько важен, что очень мало алгебры, выходящей за рамки этого пункта, может быть достигнуто без понимания этого.
В предыдущих главах подчеркивалось различие между терминами и факторами .Вы должны помнить, что члены складываются или вычитаются, а множители умножаются. Далее следуют три важных определения.
Термины встречаются в указанной сумме или разнице. Факторы встречаются в указанном продукте.
Выражение в факторизованной форме только в том случае, если все выражение является указанным продуктом.

Обратите внимание, что в этих примерах мы всегда должны рассматривать все выражение целиком. Факторы могут состоять из терминов, а термины могут содержать факторы, но фактор из должен соответствовать приведенному выше определению.
Факторинг — это процесс преобразования выражения суммы или разности членов в произведение факторов.
Обратите внимание, что в этом определении подразумевается, что значение выражения не изменяется — изменяется только его форма.
УДАЛЕНИЕ ОБЩИХ ФАКТОРОВ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Определите, какие факторы являются общими для всех терминов в выражении.
- Фактор общие множители.
В предыдущей главе мы умножили такое выражение, как 5 (2x + 1), чтобы получить 10x + 5. В общем, факторинг «отменит» умножение. Каждый член 10x + 5 имеет множитель 5, а 10x + 5 = 5 (2x + 1).
Чтобы разложить выражение на множители путем удаления общих множителей, действуйте, как в примере 1.

3x — наибольший общий делитель всех трех членов. Затем найдите факторы, общие для всех терминов, и найдите наибольший из них.Это самый общий фактор. В этом случае наибольший общий делитель равен 3x.
Поставьте 3x перед круглыми скобками.
Термины в круглых скобках находятся путем деления каждого члена исходного выражения на 3x.
Обратите внимание, что это свойство распределения. Это процесс, обратный тому, что мы использовали до сих пор. Исходное выражение теперь преобразовано в факторизованную форму.Чтобы проверить факторинг, имейте в виду, что факторинг изменяет форму, но не значение выражения. Если ответ правильный, это должно быть правдой. Умножьте, чтобы убедиться, что это правда. Вторая проверка также необходима для факторинга — мы должны быть уверены, что выражение было полностью факторизовано.
 Другими словами, «Мы удалили все общие факторы? Можем ли мы использовать дополнительные факторы?»
Другими словами, «Мы удалили все общие факторы? Можем ли мы использовать дополнительные факторы?»Если бы мы только удалили множитель «3» из 3x 2 + 6xy + 9xy 2 , ответ был бы
3 (х 2 + 2xy + 3xy 2 ).
Умножая для проверки, мы обнаруживаем, что ответ фактически совпадает с исходным выражением. Однако фактор x по-прежнему присутствует во всех терминах. Следовательно, выражение не учитывается полностью.
Это выражение факторизовано, но не полностью. Чтобы факторинг был правильным, решение должно соответствовать двум критериям:
- Должна быть возможность умножить факторизованное выражение и получить исходное выражение.
- F Выражение должно быть полностью разложено на множителя.
Пример 2 Фактор 12x 3 + 6x 2 + 18x.
Решение
На этом этапе нет необходимости перечислять факторы каждого семестра.
 Вы должны уметь мысленно определить наиболее общий фактор. Хорошая процедура — думать об элементах по отдельности. Другими словами, не пытайтесь получить все общие множители сразу, а получите сначала число, а затем каждую задействованную букву.Например, 6 — множитель 12, 6 и 18, а x — множитель каждого члена. Следовательно, 12x 3 + 6x 2 + 18x = 6x (2x 2 + x + 3). Умножая, мы получаем оригинал и видим, что члены в круглых скобках не имеют другого общего множителя, поэтому мы знаем, что решение правильное.
Вы должны уметь мысленно определить наиболее общий фактор. Хорошая процедура — думать об элементах по отдельности. Другими словами, не пытайтесь получить все общие множители сразу, а получите сначала число, а затем каждую задействованную букву.Например, 6 — множитель 12, 6 и 18, а x — множитель каждого члена. Следовательно, 12x 3 + 6x 2 + 18x = 6x (2x 2 + x + 3). Умножая, мы получаем оригинал и видим, что члены в круглых скобках не имеют другого общего множителя, поэтому мы знаем, что решение правильное.Скажите себе: «Каков наибольший общий делитель 12, 6 и 18?» Затем «Какой наибольший общий делитель x 3 , x 2 и x?» Помните, что это проверка, чтобы убедиться в правильности факторинга. 
Опять умножаем как чек. Снова найдите наибольший общий делитель чисел и каждой буквы отдельно. Если выражение не может быть разложено на множители, оно считается простым .
Помните, что 1 всегда является множителем любого выражения. РАЗДЕЛЕНИЕ ПО ГРУППАМ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Факторные выражения, когда общий множитель включает более одного члена.
- Фактор по группировке.
Расширение идей, представленных в предыдущем разделе, применяется к методу факторинга, который называется группировка .
Прежде всего, мы должны отметить, что общий множитель не обязательно должен быть одним членом.
 Например, в выражении 2y (x + 3) + 5 (x + 3) есть два члена. Это 2y (x + 3) и 5 (x + 3). В каждом из этих терминов есть множитель (x + 3), состоящий из членов. Этот множитель (x + 3) является общим множителем.
Например, в выражении 2y (x + 3) + 5 (x + 3) есть два члена. Это 2y (x + 3) и 5 (x + 3). В каждом из этих терминов есть множитель (x + 3), состоящий из членов. Этот множитель (x + 3) является общим множителем.Иногда, когда имеется четыре или более терминов, мы должны вставить один или два промежуточных шага, чтобы разложить их на множители.
Решение
Прежде всего отметьте, что не все четыре члена в выражении имеют общий множитель, но некоторые из них имеют. Например, мы можем умножить на 3 первые два члена, получив 3 (ax + 2y). Если мы вычленим a из оставшихся двух членов, мы получим a (ax + 2y). Выражение теперь 3 (ax + 2y) + a (ax + 2y), и у нас есть общий множитель (ax + 2y), и мы можем разложить на множители как (ax + 2y) (3 + a). Умножая (ax + 2y) (3 + a), мы получаем исходное выражение 3ax + 6y + a 2 x + 2ay и видим, что факторизация верна.
Это пример факторинга путем группировки , поскольку мы «сгруппировали» термины по два за раз.

Умножьте (x — y) (a + 2) и посмотрите, получите ли вы исходное выражение.
Опять умножаем как чек.Иногда термины необходимо сначала переставить, прежде чем можно будет выполнить факторинг по группировке.
Пример 7 Фактор 3ax + 2y + 3ay + 2x.
Решение
Первые два члена не имеют общего множителя, но первое и третье члены имеют, поэтому мы изменим порядок членов, чтобы поместить третий член после первого.Всегда смотрите вперед, чтобы увидеть порядок, в котором можно расположить термины.
Во всех случаях важно быть уверенным, что факторы, указанные в скобках, абсолютно одинаковы. Это может потребовать факторизации отрицательного числа или буквы.
Помните, свойство коммутативности позволяет нам переставлять эти члены.
Умножение как проверка.
Пример 8 Фактор ax — ay — 2x + 2y.
Решение
Обратите внимание, что когда мы множим a из первых двух членов, мы получаем a (x — y).Глядя на последние два члена, мы видим, что разложение на множители +2 дает 2 (-x + y), а разложение на множители «-2» дает -2 (x — y). Мы хотим, чтобы члены в круглых скобках были (x — y), поэтому поступаем таким же образом.
ФАКТОРИНГ ТРИНОМИНАЛА
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Мысленно перемножьте два бинома.
- Разложите на множители трехчлена с коэффициентом первого члена, равным 1.
- Найдите множители любого факторизуемого трехчлена.
Большое количество будущих проблем будет связано с факторизацией трехчленов как произведения двух биномов. В предыдущей главе вы узнали, как умножать многочлены. Теперь мы хотим рассмотреть частный случай умножения двух биномов и разработать образец для этого типа умножения.

Поскольку этот тип умножения очень распространен, полезно иметь возможность найти ответ, не выполняя так много шагов. Давайте посмотрим на образец для этого.
Из примера (2x + 3) (3x — 4) = 6x 2 + x — 12, обратите внимание, что первый член ответа (6x 2 ) был получен из произведения двух первых членов множителей. , то есть (2x) (3x).
Также обратите внимание, что третий член (-12) произошел от произведения вторых членов множителей, то есть (+ 3) (-4).
Теперь у нас есть следующая часть узора:
Теперь, снова посмотрев на пример, мы видим, что средний член (+ x) получен из суммы двух произведений (2x) (-4) и (3) (3x).
Теперь у нас есть четыре произведения для любых двух биномов:
- Первый семестр за первый семестр
- Внешние условия
- Внутренние условия
- Последний семестр к последнему семестру
Эти продукты показаны этим шаблоном.

Когда произведения внешних и внутренних терминов дают одинаковые термины, их можно комбинировать, и решение является трехчленом.
Этот метод умножения двух биномов иногда называют методом FOIL.
FOIL расшифровывается как «первый», «внешний», «внутренний», «последний».
Это сокращенный метод умножения двух биномов, и его полезность станет очевидной, когда мы разложим на множители трехчлены.Вы должны запомнить этот образец.
Опять же, возможно, вам поможет запоминание слова FOIL. Не только этот образец должен быть запомнен, но ученик должен также научиться переходить от проблемы к ответу без каких-либо письменных шагов.Этот умственный процесс умножения необходим, если мы хотим достичь мастерства в факторинге.
Выполняя следующие упражнения, попытайтесь прийти к правильному ответу, не записывая ничего, кроме ответа.
 Чем больше вы будете практиковать этот процесс, тем лучше будете в факторинге.
Чем больше вы будете практиковать этот процесс, тем лучше будете в факторинге.Теперь, когда мы установили образец умножения двух биномов, мы готовы разложить на множители трехчлены. Сначала мы рассмотрим факторизацию только тех трехчленов с коэффициентом первого члена, равным 1.
Решение
Поскольку это трехчлен и не имеет общего множителя, мы будем использовать шаблон умножения для разложения.
Фактически мы будем работать в обратном порядке, как в предыдущем наборе упражнений. Сначала в скобках укажите проблему.
Теперь мы хотим заполнить члены так, чтобы шаблон давал исходный трехчлен при умножении. Первый член прост, поскольку мы знаем, что (x) (x) = x 2 .
Помните, произведение первых двух членов двучлена дает первый член трехчлена. 
Теперь мы должны найти числа, которые умножаются, чтобы получить 24, и в то же время складывать, чтобы получить средний член. Обратите внимание, что в каждом из следующих слов будут правильные первый и последний член.
Только последний продукт имеет средний член 11x, и правильное решение —
Этот метод факторинга называется методом проб и ошибок — по понятным причинам.
Здесь могут быть полезны некоторые числовые факты из арифметики. - Произведение двух нечетных чисел является нечетным.
- Произведение двух четных чисел является четным.
- Произведение четного и нечетного числа является четным.
- Сумма двух нечетных чисел четная.
- Сумма двух четных чисел четная.
- Сумма нечетного и четного числа нечетная.

Таким образом, будут работать только нечетное и четное число. Нам даже не нужно пробовать такие комбинации, как 6 и 4, 2 и 12 и так далее.Решение
Здесь проблема лишь немного в другом. Мы должны найти числа, которые умножаются, чтобы получить 24, и в то же время складывать, чтобы получить — 11. Вы всегда должны помнить об этой схеме. Последний член получается строго умножением, а средний член, в конечном итоге, получается из суммы. Зная, что произведение двух отрицательных чисел положительно, а сумма двух отрицательных чисел отрицательна, получаем
Решение
Здесь мы столкнулись с отрицательным числом для третьего члена, и это немного усложняет задачу.Поскольку -24 может быть только произведением положительного числа и отрицательного числа, и поскольку средний член должен происходить из суммы этих чисел, мы должны мыслить категориями разницы. Мы должны найти числа, произведение которых равно 24 и которые отличаются на 5.
 Кроме того, большее число должно быть отрицательным, потому что, когда мы складываем положительное и отрицательное число, ответ будет иметь знак большего. Учитывая все это, получаем
Кроме того, большее число должно быть отрицательным, потому что, когда мы складываем положительное и отрицательное число, ответ будет иметь знак большего. Учитывая все это, получаемПорядок коэффициентов несущественный.
по коммутативному закону умножения.Следующие пункты помогут при факторизации трехчленов:
- Когда знак третьего члена положительный, оба знака в множителях должны быть одинаковыми — и они должны быть похожи на знак среднего члена.
- Когда знак последнего члена отрицательный, знаки в множителях должны быть разными, а знак большего члена должен быть подобен знаку среднего члена.
В предыдущем упражнении коэффициент каждого из первых членов был равен 1.Когда коэффициент при первом члене не равен 1, проблема факторинга намного сложнее, потому что количество возможностей значительно увеличивается.
Выполнив предыдущий набор упражнений, теперь вы готовы попробовать еще несколько сложных трехчленов. 
Обратите внимание, что существует двенадцать способов получить первый и последний члены, но только один имеет 17x в качестве среднего члена.
Вы, конечно, можете попробовать каждый из них мысленно, вместо того, чтобы записывать их. Есть только один способ получить все три условия:
В этом примере верна одна из двенадцати возможностей. Таким образом, метод проб и ошибок может занять очень много времени.
Даже несмотря на то, что используемый метод представляет собой метод предположений, это должно быть «обоснованное предположение», в котором мы применяем все наши знания о числах и много упражняемся в мысленной арифметике. В предыдущем примере мы сразу отбросили бы многие комбинации.Поскольку мы ищем 17x как средний термин, мы не будем пытаться использовать те возможности, которые умножают 6 на 6, или 3 на 12, или 6 на 12, и так далее, поскольку эти произведения будут больше 17.
 Кроме того, поскольку 17 нечетное, мы знаем, что это сумма четного и нечетного числа. Все это помогает уменьшить количество возможностей попробовать.
Кроме того, поскольку 17 нечетное, мы знаем, что это сумма четного и нечетного числа. Все это помогает уменьшить количество возможностей попробовать.Сначала найдите числа, которые дают правильные первое и последнее члены трехчлена. Затем добавьте внешний и внутренний продукт, чтобы проверить правильность среднего срока. Решение
Сначала мы должны проанализировать проблему.
- Последний член положительный, поэтому два одинаковых знака.
- Средний член отрицательный, поэтому оба знака будут отрицательными.
- Множители 6×2: x, 2x, 3x, 6x. Множители 15: 1, 3, 5, 15.
- Исключите как слишком большое произведение 15 с 2x, 3x или 6x. Попробуйте несколько разумных комбинаций.
Это автоматически даст слишком большой средний член. Посмотрите, как сокращается количество возможностей. 
Решение
Анализировать:
- Последний член отрицательный, поэтому не похож на знаки.
- Мы должны найти продукты, которые отличаются на 5 с большим отрицательным числом.
- Мы исключаем произведение 4х и 6 как вероятно слишком большое.
- Попробуйте несколько комбинаций.
Помните, попробуйте мысленно различные возможные комбинации, которые являются разумными.Это процесс факторинга «методом проб и ошибок». Практикуясь, вы научитесь лучше справляться с этим процессом. (4x — 3) (x + 2): здесь средний член равен + 5x, что является правильным числом, но неправильным знаком. Будьте осторожны, чтобы не принимать это как решение, но поменяйте знаки так, чтобы более крупный продукт соответствовал знаку со средним условием.
К тому времени, когда вы закончите следующий набор упражнений, вы почувствуете себя гораздо более комфортно при факторинге трехчлена. 
ОСОБЫЕ СЛУЧАИ ФАКТОРИНГА
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Определите и разложите на множители двух полных квадратов.
- Определите и разложите на множители трехчлен полного квадрата.
В этом разделе мы хотим изучить некоторые частные случаи факторинга, которые часто возникают в задачах. Если признать эти особые случаи, факторинг значительно упростится.
Первый частный случай, который мы обсудим, — это разность двух полных квадратов .
Напомним, что при умножении двух биномов на образец средний член получается из суммы двух произведений.
Из нашего опыта работы с числами мы знаем, что сумма двух чисел равна нулю только в том случае, если два числа являются отрицательными по отношению друг к другу.
Когда сумма двух чисел равна нулю, одно из чисел называется , аддитивно обратным другого. 
Например: (+ 3) + (-3) = 0, поэтому + 3 является аддитивным обратным значением -3, также -3 является аддитивным обратным значением +3.В каждом примере средний член равен нулю. Обратите внимание, что если два бинома умножаются, чтобы получить бином (средний член отсутствует), они должны быть в форме (a — b) (a + b).
Правило можно записать как = (a — b) (a + b). Это форма, которую вы найдете наиболее полезной при факторинге. Чтение этого правила справа налево говорит нам, что если у нас есть проблема, которую нужно разложить на множители, и если она имеет форму, то множители будут (a — b) (a + b).
Решение
Здесь оба члена представляют собой полные квадраты, разделенные знаком минус.
Особые случаи действительно упрощают факторинг, но не забывайте осознавать, что особый случай — это просто особенный случай.
 В этом случае оба члена должны быть полными квадратами, а знак должен быть отрицательным, отсюда «разница двух полных квадратов».
В этом случае оба члена должны быть полными квадратами, а знак должен быть отрицательным, отсюда «разница двух полных квадратов».Сумма двух квадратов не разложима. Вы также должны быть осторожны при распознавании идеальных квадратов.Помните, что точные квадратные числа — это числа, у которых квадратные корни являются целыми числами. Кроме того, показатели абсолютного квадрата четны.
Студенты часто упускают из виду тот факт, что (1) — это идеальный квадрат. Таким образом, такое выражение, как x 2 — 1, представляет собой разность двух полных квадратов и может быть разложено на множители этим методом. Другой частный случай факторизации — это трехчлен полного квадрата. Обратите внимание, что возведение бинома в квадрат приводит к этому случаю.
Мы признаем этот случай по его особенностям.
 Очевидны три вещи.
Очевидны три вещи.- Первый член представляет собой полный квадрат.
- Третий член представляет собой полный квадрат.
- Средний член — это дважды произведение квадратного корня из первого и третьего членов.
Для целей факторинга более полезно записать отчет как Решение
- 25x 2 — это полный квадратный корень с главным квадратным корнем = 5x.
- 4 — это полный квадратный корень из главного квадрата = 2.
- 20x — это дважды произведение квадратных корней 25x 2 и
- 20x = 2 (5x) (2).
Чтобы разложить на множители полный квадрат трехчлена , сформируйте бином с квадратным корнем из первого члена, квадратным корнем из последнего члена и знаком среднего члена и укажите квадрат этого бинома.
Таким образом, 25x 2 + 20x + 4 = (5x + 2) 2
Всегда возводите двучлен в квадрат для проверки правильности среднего члена. 
Не частный случай трехчлена полного квадрата.
ДОПОЛНИТЕЛЬНЫЕ ЯРЛЫКИ ДЛЯ ИСПЫТАНИЙ И УСТАНОВЛЕНИЕ ОШИБОК
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Найдите ключевое число трехчлена.
- Используйте ключевое число для разложения трехчлена на множители.
В этом разделе мы хотим обсудить несколько сокращений для факторинга методом проб и ошибок. Это необязательно по двум причинам. Во-первых, некоторые могут предпочесть пропустить эти методы и просто использовать метод проб и ошибок; во-вторых, эти ярлыки не всегда практичны для большого количества людей.Однако они повысят скорость и точность для тех, кто их освоит.
Первым шагом в использовании этих ярлыков является поиск ключевого номера . После того, как вы нашли ключевой номер, его можно использовать более чем одним способом.
В трехчлене, подлежащем разложению, ключевое число является произведением коэффициентов первого и третьего членов.

Произведение этих двух чисел и есть «ключевой номер».Первое использование ключевого числа показано в примере 3.
Решение
Шаг 1 Найдите ключевой номер. В этом примере (4) (- 10) = -40.
Шаг 2 Найдите множители ключевого числа (-40), которые складываются, чтобы получить коэффициент среднего члена (+ 3). В этом случае (+ 8) (-5) = -40 и (+ 8) + (-5) = +3.
Шаг 3 Коэффициенты (+ 8) и (- 5) будут перекрестными произведениями в шаблоне умножения.
Произведение этих двух чисел является ключевым числом.»
Шаг 4 Используя только внешнее перекрестное произведение, найдите множители первого и третьего членов, которые будут умножаться, чтобы получить произведение. В этом примере мы должны найти множители 4×2 и -10, которые будут умножаться, чтобы дать + 8x. Это 4x от 4×2 и (+ 2) от (-10).
Это 4x от 4×2 и (+ 2) от (-10).
Поместите эти множители в первую и последнюю позиции в шаблоне
Есть только один способ сделать это правильно.
Шаг 5 Забудьте на этом этапе номер ключа и посмотрите на исходную проблему.Поскольку первая и последняя позиции заполнены правильно, теперь необходимо заполнить только две другие позиции.
Опять же, это можно сделать только одним способом.
Мы знаем, что произведение двух первых членов должно давать 4x 2 и 4x уже на месте. Нет другого выбора, кроме x.
Обратите внимание, что на шаге 4 мы могли бы начать с внутреннего продукта вместо внешнего продукта. Мы получили бы те же множители.Самое главное — иметь систематический процесс факторинга. 
Мы знаем, что произведение двух вторых членов должно быть (-10), а (+2) уже на месте. У нас нет другого выбора, кроме (- 5).Помните, что если трехчлен факторизуем, существует только один возможный набор факторов. Если не удается найти множители ключевого числа, сумма которых является коэффициентом средних членов, то трехчлен является простым и не множится. Второе использование номера ключа в качестве ярлыка включает факторинг по группировке. Работает как в примере 5.
Решение
Шаг 1 Найдите номер ключа (4) (- 10) = -40.
Шаг 2 Найдите множители (- 40), которые складываются, чтобы получить коэффициент среднего члена (+3).Шаги 1 и 2 в этом методе такие же, как и в предыдущем методе. 
Шаг 3 Перепишите исходную задачу, разбив средний член на две части, найденные на шаге 2.8x — 5x = 3x, поэтому мы можем написать
Step 4 Разложите эту задачу на множители, начиная с шага 3, с помощью метода группировки, изученного в разделе 8-2
Теперь это становится обычным факторингом путем группировки.
Следовательно,Опять же, есть только одна возможная пара множителей, которая может быть получена из данного трехчлена. Помните, что если шаг 2 невозможен, трехчлен является простым и не может быть разложен на множители. ПОЛНАЯ ФАКТОРИЗАЦИЯ
ЗАДАЧИ
По завершении этого раздела вы сможете разложить на множители трехчлен, выполнив следующие два шага:
- Первый взгляд на общие факторы.

- Разложите оставшийся трехчлен на множители, применяя методы этой главы.
Теперь мы изучили все обычные методы факторизации в элементарной алгебре. Однако вы должны знать, что для решения одной проблемы может потребоваться более одного из этих методов.Помните, что есть две проверки правильности факторинга.
- Умножатся ли множители, чтобы получить исходную задачу?
- Все ли множители просты?
После того, как общий множитель был найден, вы должны проверить, можно ли разложить полученный трехчлен на факторизацию. Если у трехчлена есть общие множители, обычно проще, если они сначала разложены на множители. Хорошая процедура, которой следует придерживаться при факторинге, — всегда сначала удалять наибольший общий множитель, а затем, если возможно, разложить на множители то, что осталось.

РЕЗЮМЕ
Ключевые слова
- Выражение в факторизованной форме только в том случае, если все выражение является указанным продуктом.
- Факторинг — это процесс, который изменяет сумму или разность условий на произведение факторов.
- Простое выражение не может быть разложено на множители.
- Наибольший общий множитель — наибольший общий множитель для всех терминов.
- Выражение полностью разложено на множители , когда дальнейшее разложение на множители невозможно.
- Возможность факторизации путем группировки существует, когда выражение содержит четыре или более терминов.
- Метод FOIL можно использовать для умножения двух биномов.
- Частные случаи факторинга включают разность двух квадратов и трехчленов полного квадрата .
- Ключевое число является произведением коэффициентов первого и третьего членов трехчлена.




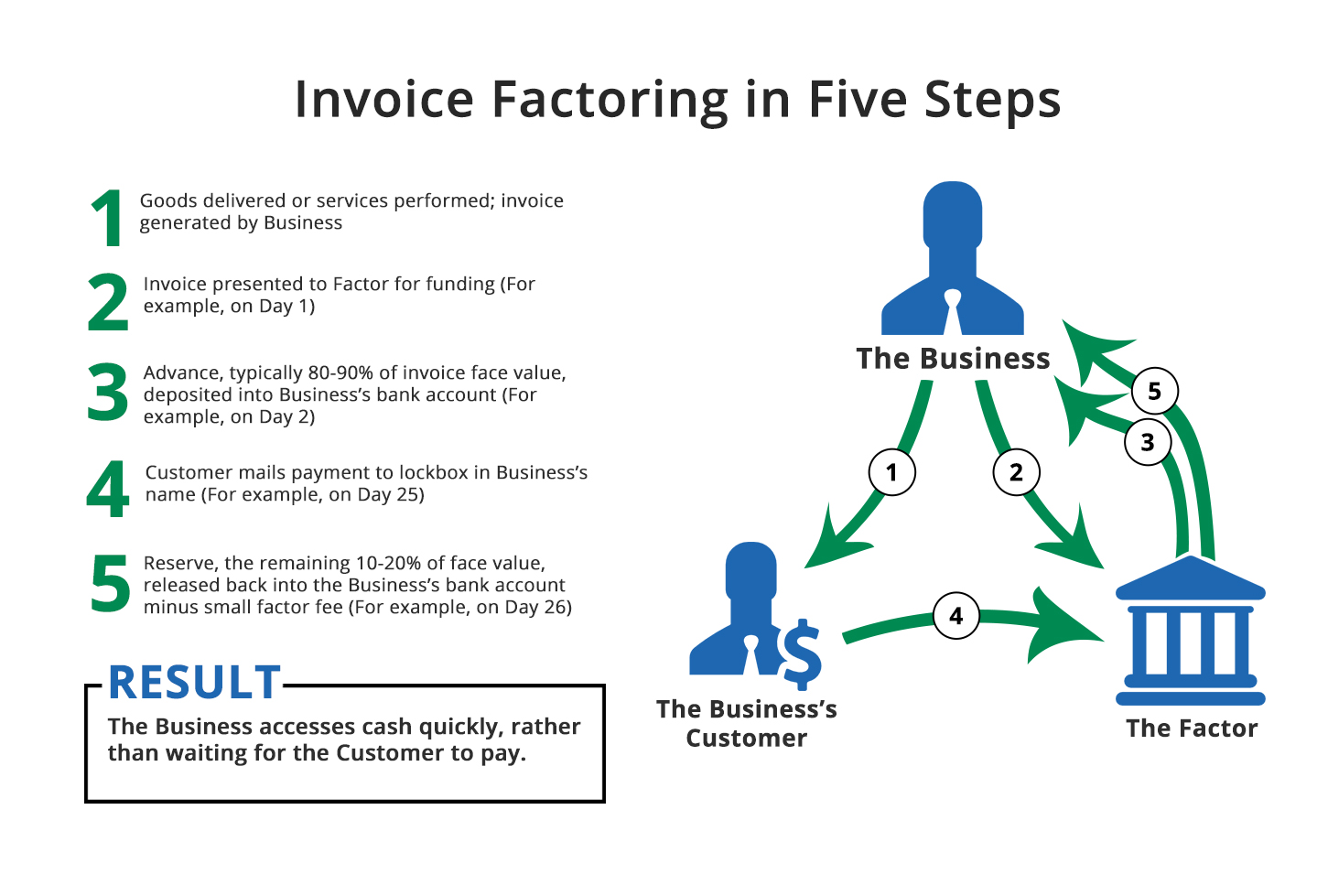
 {2} +7 x + 3 \).{2} +15 х-27 \)
{2} +7 x + 3 \).{2} +15 х-27 \)
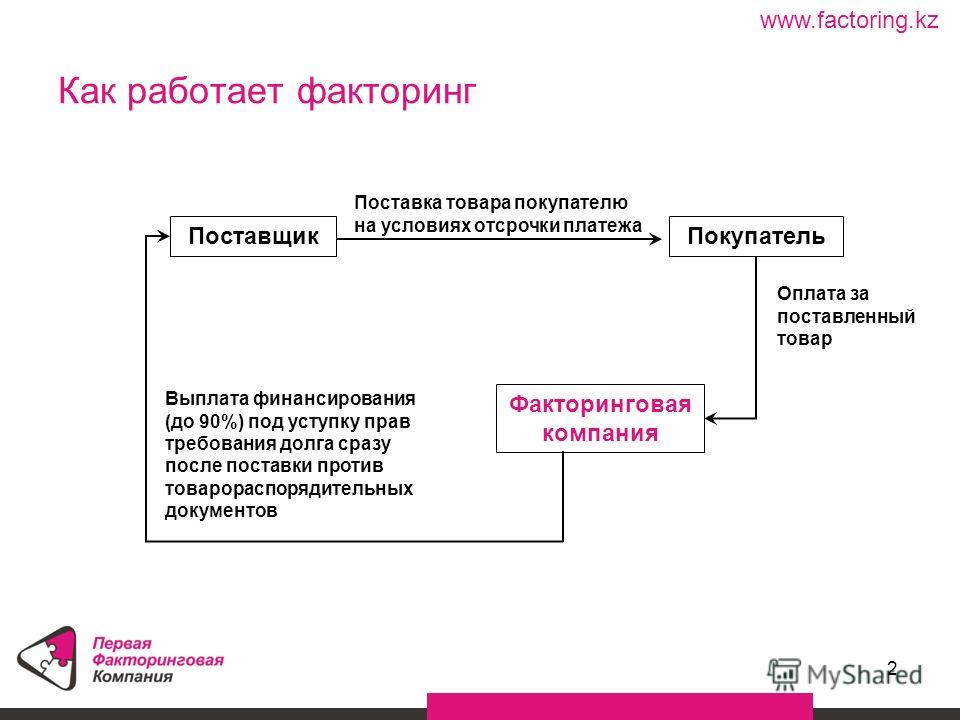 Подсчитайте количество членов многочлена: если многочлен состоит из двух членов, попробуйте формулу разности двух квадратов; если многочлен состоит из трех членов, попробуйте AC-метод; если многочлен состоит из четырех членов, попробуйте метод группировки.{2} -10 х + 3 \)
Подсчитайте количество членов многочлена: если многочлен состоит из двух членов, попробуйте формулу разности двух квадратов; если многочлен состоит из трех членов, попробуйте AC-метод; если многочлен состоит из четырех членов, попробуйте метод группировки.{2} -10 х + 3 \)
 Факторы, такие как стабильность бизнеса, а также отрасль бизнеса и история транзакций, обычно определяют потенциальные ставки аванса.
Факторы, такие как стабильность бизнеса, а также отрасль бизнеса и история транзакций, обычно определяют потенциальные ставки аванса. Например, ставка фактора может начинаться с 1%, увеличиваться до 2% на второй неделе и до 5% на третьей неделе. В качестве альтернативы ставка может начинаться с 2% и оставаться на этом уровне в течение первых 30 дней, после этого увеличиваясь с заданными приращениями.
Например, ставка фактора может начинаться с 1%, увеличиваться до 2% на второй неделе и до 5% на третьей неделе. В качестве альтернативы ставка может начинаться с 2% и оставаться на этом уровне в течение первых 30 дней, после этого увеличиваясь с заданными приращениями. По этой причине договоры факторинга без права регресса обычно более дороги и предназначены для отраслей, которые представляют меньший риск для факторинговых компаний.
По этой причине договоры факторинга без права регресса обычно более дороги и предназначены для отраслей, которые представляют меньший риск для факторинговых компаний.

 Другими словами, «Мы удалили все общие факторы? Можем ли мы использовать дополнительные факторы?»
Другими словами, «Мы удалили все общие факторы? Можем ли мы использовать дополнительные факторы?»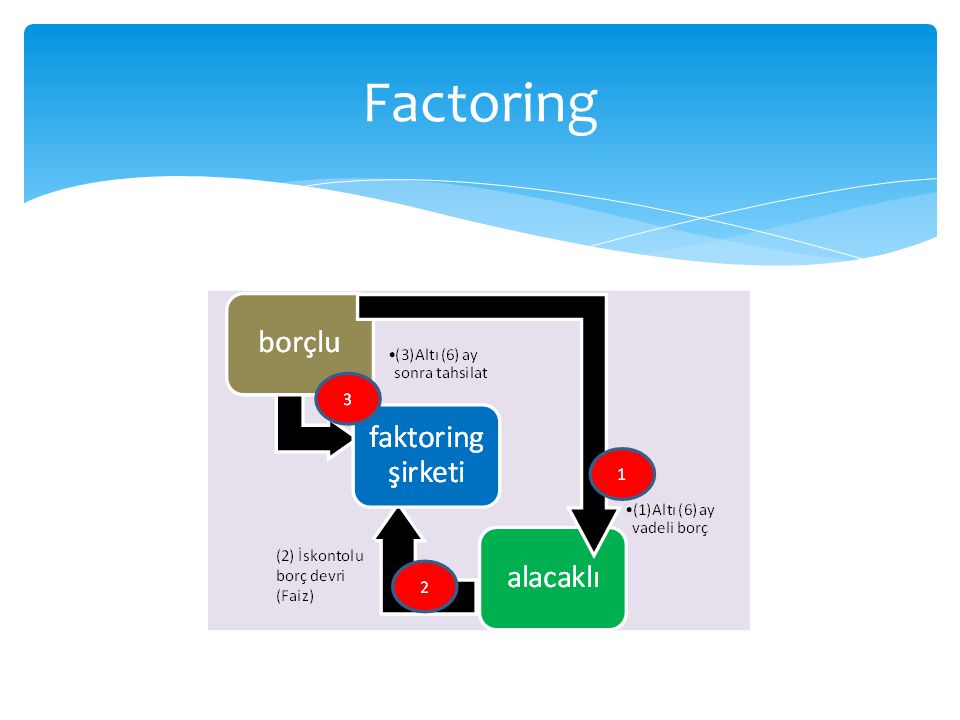 Вы должны уметь мысленно определить наиболее общий фактор. Хорошая процедура — думать об элементах по отдельности. Другими словами, не пытайтесь получить все общие множители сразу, а получите сначала число, а затем каждую задействованную букву.Например, 6 — множитель 12, 6 и 18, а x — множитель каждого члена. Следовательно, 12x 3 + 6x 2 + 18x = 6x (2x 2 + x + 3). Умножая, мы получаем оригинал и видим, что члены в круглых скобках не имеют другого общего множителя, поэтому мы знаем, что решение правильное.
Вы должны уметь мысленно определить наиболее общий фактор. Хорошая процедура — думать об элементах по отдельности. Другими словами, не пытайтесь получить все общие множители сразу, а получите сначала число, а затем каждую задействованную букву.Например, 6 — множитель 12, 6 и 18, а x — множитель каждого члена. Следовательно, 12x 3 + 6x 2 + 18x = 6x (2x 2 + x + 3). Умножая, мы получаем оригинал и видим, что члены в круглых скобках не имеют другого общего множителя, поэтому мы знаем, что решение правильное.




 Чем больше вы будете практиковать этот процесс, тем лучше будете в факторинге.
Чем больше вы будете практиковать этот процесс, тем лучше будете в факторинге.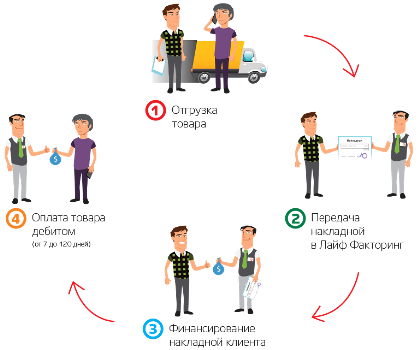

 Кроме того, большее число должно быть отрицательным, потому что, когда мы складываем положительное и отрицательное число, ответ будет иметь знак большего. Учитывая все это, получаем
Кроме того, большее число должно быть отрицательным, потому что, когда мы складываем положительное и отрицательное число, ответ будет иметь знак большего. Учитывая все это, получаем
 Кроме того, поскольку 17 нечетное, мы знаем, что это сумма четного и нечетного числа. Все это помогает уменьшить количество возможностей попробовать.
Кроме того, поскольку 17 нечетное, мы знаем, что это сумма четного и нечетного числа. Все это помогает уменьшить количество возможностей попробовать.


 В этом случае оба члена должны быть полными квадратами, а знак должен быть отрицательным, отсюда «разница двух полных квадратов».
В этом случае оба члена должны быть полными квадратами, а знак должен быть отрицательным, отсюда «разница двух полных квадратов».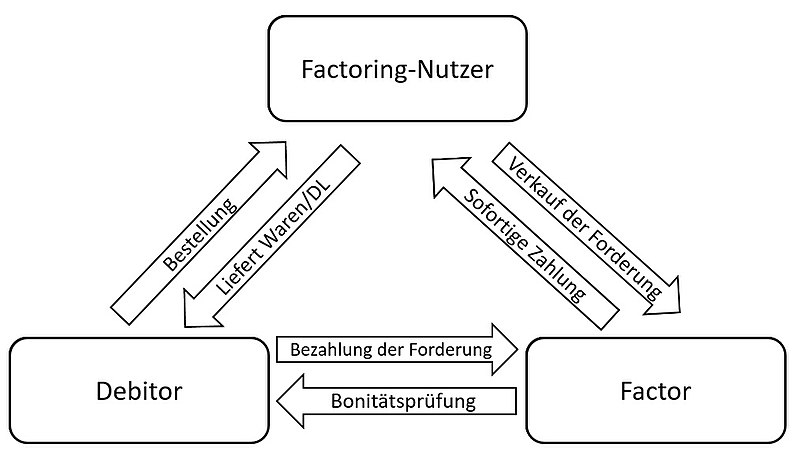 Очевидны три вещи.
Очевидны три вещи.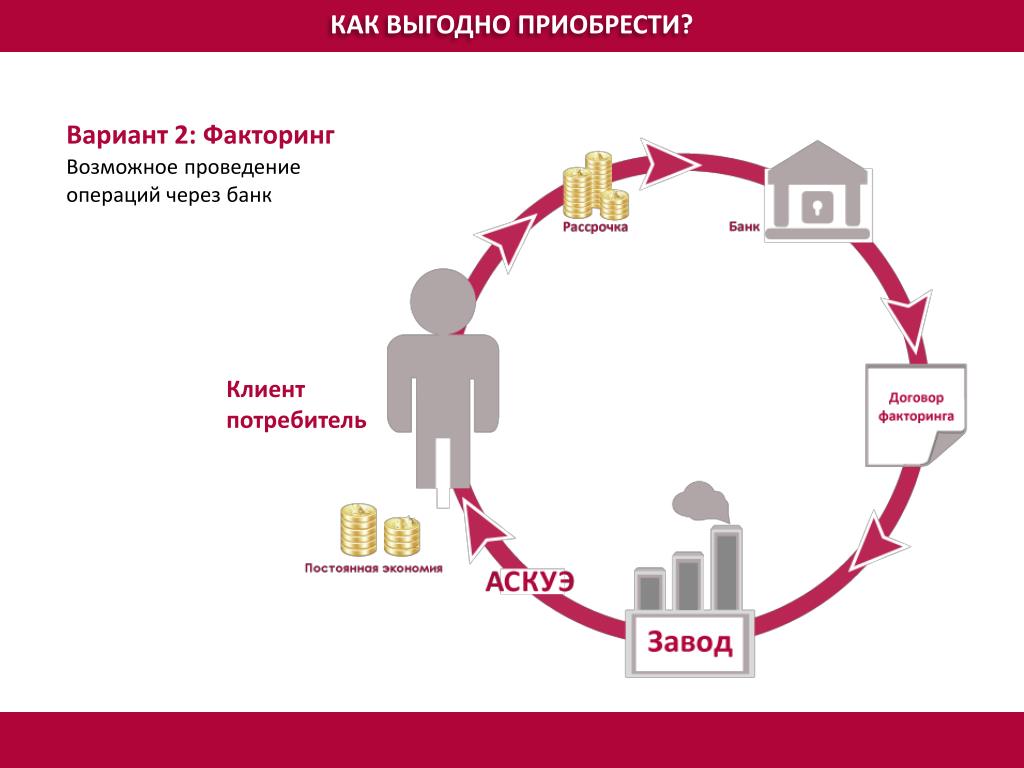

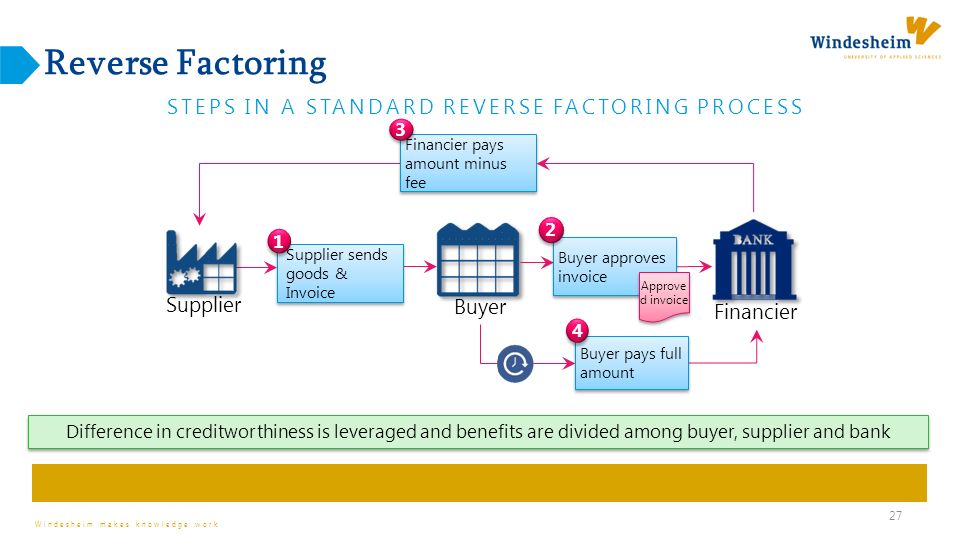 Это 4x от 4×2 и (+ 2) от (-10).
Это 4x от 4×2 и (+ 2) от (-10). 

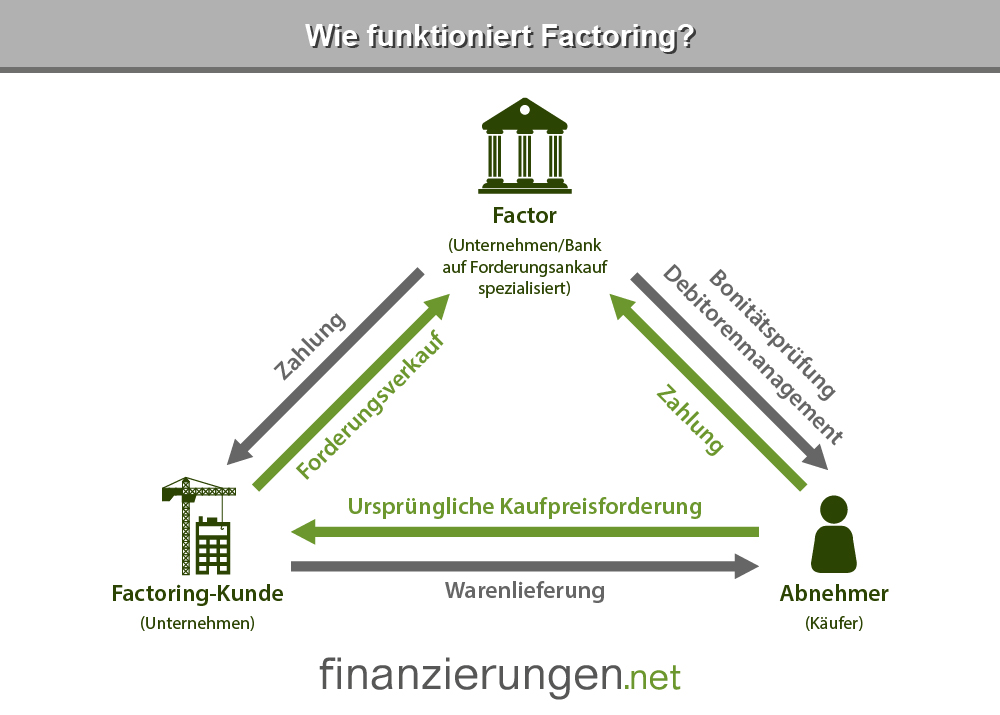


Добавить комментарий
Комментарий добавить легко