Как посчитать процент от числа и долю в Эксель

Расчеты с процентами – относятся к одним из самых популярных действий, выполняемых в программе Эксель. Это может быть умножение числа на определенный процент, определение доли (в %) от конкретного числа и т.д. Однако, даже если пользователь знает, как выполнить расчеты на листке бумаги, он не всегда может повторить их в программе. Потому сейчас, мы детально разберем, как именно считаются проценты в Эксель.

Считаем долю от общего числа

Для начала разберем довольно распространенную ситуацию, когда нам нужно определить долю одного числа (в процентах) в другом. Ниже приведена математическая формула для выполнения данной задачи:

Доля (%) = Число 1/Число 2*100%, где:

• Число 1 – собственно говоря, наше исходное числовое значение
• Число 2 – итоговое число, долю в котором мы хотим выяснить

К примеру, давайте попробуем вычислить, какова доля числа 15 в числе 37.

Результат нам нужен в процентах. В данном значение “Числа 1” равно 15, а “Числа 2” – 37.

1. Выбираем ячейку, где нам нужно произвести расчеты. Пишем знак “равно” (“=”) и далее формулу расчета с нашими числами: =15/37*100%.
2. После того, как мы набрали формулу, нажимаем клавишу Enter на клавиатуре, и результат сразу же отобразится в выбранной ячейке.

У некоторых пользователей в результирующей ячейке вместо процентного значения может отобразится простое число, причем, иногда с большим количеством цифр после запятой.

Все дело в том, что не настроен формат ячейки для вывода результата. Давайте это исправим:

1. Кликаем правой кнопкой мыши по ячейке с результатом (неважно, до того, как мы написали в ней формулу и получили результат или после), в появившемся перечне команд щелкаем по пункту “Формат ячеек…”.
2. В окне форматирования мы окажемся во вкладке “Число”. Здесь в числовых форматах кликаем по строке “Процентный” и в правой части окна указываем желаемое количество знаков после запятой. Наиболее распространенный вариант – “2”, его мы и ставим в нашем примере. После этого жмем кнопку OK.
3. Готово, теперь мы получим в ячейке именно процентное значение, что и требовалось изначально.

Кстати, когда формат отображения в ячейке настроен в виде процентов, вовсе не обязательно в формуле писать “*100%“. Достаточно будет выполнить простое деление чисел: =15/37.

Давайте попробуем применить полученные знания на практике. Допустим, у нас есть таблица с продажами по различным наименованиям, и нам нужно вычислить долю каждого товара в суммарной выручке. Для удобства лучше вывести данные в отдельный столбец. Также, у нас должна быть заранее посчитана итоговая выручка по всем наименованиям, на которую мы будем делить продажи по каждому товару.

Итак, приступим к выполнению поставленной задачи:

1. Выбираем первую ячейку столбца (не считая шапку таблицы). Как обычно, написание любой формулы начинается со знака “=“. Далее пишем формулу расчета процента, аналогично рассмотренному примеру выше, только заменив конкретные числовые значения адресами ячеек, которые можно прописать вручную, либо добавляем их в формулу кликами мыши. В нашем случае, в ячейку E2 нужно написать следующее выражение: =D2/D16. Примечание: не забываем заранее настроить формат ячеек результирующего столбца, выбрав отображение в виде процентов.
2. Нажимаем Enter, чтобы получить результат в заданной ячейке.
3. Теперь нам нужно произвести аналогичные расчеты для остальных строк столбца. К счастью, возможности Эксель позволяют избежать ручного ввода формулы для каждой ячейки, и этот процесс можно автоматизировать путем копирования (растягивания) формулы в другие ячейки. Однако тут есть небольшой нюанс. В программе по умолчанию при копировании формул происходит корректировка адресов ячеек согласно смещению. Когда речь идет о продажах каждого отдельного наименования, так и должно быть, но координаты ячейки с итоговой выручкой должны оставаться неизменными. Чтобы ее зафиксировать (сделать абсолютной), нужно перед обозначениями строки и столбца добавить символ “ $“. Либо, чтобы не печатать этот знак вручную, выделив адрес ячейки в формуле, можно просто нажать клавишу F4. По завершении нажимаем Enter.
4. Теперь осталось растянуть формулу на другие ячейки. Чтобы это сделать, наводим курсор на правый нижний угол ячейки с результатом, указатель должен поменять форму на крестик, после чего, растягиваем формулу вниз, зажав левую кнопку мыши.
5. Вот и все. Как мы и хотели, ячейки последнего столбца заполнились долями продаж каждого конкретного наименования продукции в совокупной выручке.

Разумеется, в расчетах вовсе не обязательно заранее считать итоговую выручку и выводить результат в отдельную ячейку. Все можно сразу посчитать с помощью одной формулы, которая для ячейки

E2 выглядеть так: =D2/СУММ(D2:D15).

В данном случае, мы сразу посчитали общую выручку в формуле расчета доли, используя функцию СУММ. О том, как ее применять, читайте в нашей статье – “Как в Экселе посчитать сумму ячеек“.

Как и в первой варианте, нам нужно зафиксировать цифру по итоговым продажам, однако, так как в расчетах не принимает участие отдельная ячейка с нужным значением, нам нужно проставить знаки “

$” перед обозначениями строк и столбцов в адресах ячеек диапазона суммы: =D2/СУММ($D$2:$D$15).

Находим процент от числа

А сейчас давайте попробуем вычислить процент от числу в виде абсолютного значения, т.е. в виде другого числа.

Математическая формула для расчета выглядит следующим образом:

Число 2 = Процент (%) * Число 1, где:

• Число 1 – исходное число, процент по которому нужно вычислить
• Процент – соответсвенно, величина самого процента
• Число 2 – финальное числовое значение, которое требуется получить.

Например, давайте узнаем, какое число составляет 15% от 90.

1. Выбираем ячейку, в которой будем выводить результат и пишем формулу выше, подставляя в нее наши значения: =15%*90. Примечание: Так как результат должен быть в абсолютном выражении (т.е. в виде числа), формат ячейки – “общий” или “числовой” (но не “процентный”).
2. Нажимаем клавишу Enter, чтобы получить результат в выбранной ячейке.

Подобные знания помогают решать множество математических, экономических задач, физических и других задач. Допустим, у нас есть таблица с продажами обуви (в парах) за 1 квартал, и мы планируем в следующем продать на 10% больше. Нужно определить, какому количеству пар для каждого наименования соответствуют эти 10%.

Чтобы выполнить задачу, выполняем следующие шаги:

1. Для удобства создаем новый столбец, в ячейки которого будем выводить результаты расчетов. Выбираем первую ячейку столбца (на считая шапки) и пишем в ней формулу выше, заменив конкретное значение сходного числа на адрес ячейки: =10%*B2.
2. После этого жмем клавишу Enter, и результат сразу же отобразится в ячейке с формулой.
3. Если мы хотим избавиться от цифр после запятой, так как в нашем случае количество пар обуви может исчисляться только целыми числами, переходим в формат ячейки (как это сделать, мы разобрали выше), где выбираем числовой формат с отсутствием десятичных знаков.
4. Теперь можно растянуть формулу на оставшиеся ячейки столбца.

В случаях, когда нам нужно получить разные проценты от разных чисел, соответственно, нужно создать отдельный столбец не только для вывода результатов, но и для значений процентов.

1. Допустим, наша таблица содержит такой столбец “E” (Значение %).
2. Пишем в первой ячейке результирующего столбца все ту же формулу, только теперь и конкретное значение процента меняем на адрес ячейки с содержащейся в ней процентной величиной: =E2*B2.
3. Щелкнув Enter получаем результат в заданной ячейке. Осталось только растянут его на нижние строки.

Заключение

Во время работы с таблицами нередко возникает потребность производить расчеты с процентами. К счастью, функционал программы Эксель позволяет выполнять их с легкостью, причем, если речь идет об однотипных вычислениях в больших таблицах, процесс можно автоматизировать, что позволит сэкономить немало времени.

Как посчитать проценты от суммы (числа)?

Потребность вычислить процент от суммы или числа может возникнуть по разным причинам: кому-то нужно узнать, насколько на самом деле выгодна предложенная магазином скидка; кому-то — подставить значение в формулу.

В любом случае последовательность действий всегда одинакова, и люди продолжают высчитывать проценты по одному и тому же алгоритму. Как это делается — попробуем разобраться.

Как посчитать проценты без калькулятора?

Процент — это буквально одна сотая часть от одного числа или суммы чисел. Высчитать один процент не сложнее, чем сделать график в Ворде: достаточно разделить исходное значение на сто. Ниже будет на примерах показано, как подсчитать процент в разных ситуациях.

Формула для расчёта процентов от числа или суммы имеет вид:

ХП = Х × Ч / 100, где

• ХП — искомые проценты;
• Х — количество процентов;
• Ч — исходное число.

Пример 1. Узнать, сколько будет 11% от 80. Расчёты осуществляются в одно действие: 11 × 80 / 100 = 88 / 100 = 8,8.

Пример 2. Вычислить 15% от суммы чисел 17 и 23. Чтобы найти результат без калькулятора, удобно разбить вычисления на три действия:

• 15% × 17 = 15 × 17 / 100 = 2,25 — для первого слагаемого.
• 15% × 23 = 15 × 23 / 100 = 3,45 — для второго слагаемого.
• 2,25 + 3,45 = 5,7 — полученная сумма.

Таким образом, 15% от суммы равно 5,7. Можно и сложить оба числа, а затем посчитать процент от результата — полученное значение будет точно таким же.

Пример 3. Найти, сколько будет 35% от разности чисел 98 и 52. Правильно считать в этом случае можно двумя способами: как в предыдущем, разбив вычисление на три действия, или сразу вычесть из первого числа второе, и узнать процент от разности: 35% × (98 — 52) = 35% × 46 = 35 × 46 / 100 = 16,1.

Пример 4. Вычесть 25% из 28. Чтобы получить результат, нужно:

• Посчитать 25 процентов от 28: 25% × 28 = 25 × 28 / 100 = 7.
• Отнять полученное значение от исходного: 28 – 7 = 21.

Итак, посчитать проценты от числа или суммы можно только одним способом — вывести какую-либо новую формулу пока ещё никому не удалось.

Чтобы облегчить вычисление, можно использовать простое правило. Формулируется оно следующим образом: А процентов от числа Б — это точно то же самое, что Б процентов от числа А. Так, 25% от 80 равно 80% от 25; убедиться в этом можно, проведя простые вычисления:

• 25% × 80 = 25 × 80 / 100 = 20.
• 80% × 25 = 80 × 25 / 100 = 20.

Как считать проценты на калькуляторе?

Калькулятор же снимает всякую необходимость в «перестановках»: посчитать с его помощью любой процент от любого числа или суммы проще, чем построить график в Excel.

Пусть требуется найти 19% от выражения (12 + 57 – 6). Порядок вычислений:

• Просуммировать все числа, последовательно вводя их с помощью клавиш.

• Нажать на клавишу «Равно», «Ввод» или аналогичную ей.

• Разделить полученное значение на 100.

• Умножить частное на количество процентов, в данном случае — 19. Вычисленное значение и будет искомым ответом: 19% от выражения (12 + 57 – 6) равно 11,97.

Совет: немного упростить задачу можно, сразу разделив 19 на 100 в уме и умножив полученное значение на сумму. Результат, как можно убедиться, ничем не отличается от ранее полученного.

Подводим итоги

Посчитать проценты от числа можно только одним способом: разделив его на сто и затем умножив на количество процентов. Производить операции можно как «на листочке», так и при помощи калькулятора. При расчётах необходимо соблюдать обычный для арифметических вычислений порядок действий.

Смотрите также

Проценты — рассчитать

На этом сайте вы всегда сможете расчитать проценты онлайн через уже готовые специальные калькуляторы моментальных вычислений. Так же вы можете узнать формулы для того чтобы расчитывать проценты самостоятельно и на обычном калькуляторе или даже в уме.

Вы можете вести расчёт онлайн, используя ниже приведённый обычный калькулятор:

Примеры вычислений онлайн с помощью калькулятора процентов

Сколько будет 13 % от числа 327

Итог — 42. 51

Как вычислять: составляем пропорцию —
327 это 100 %
икс это 13 %

Перемножаем взятые по диагонали цифры: 327 x 13 = 4251 и делим полученное произведение на 100: 4251 / 100 = 42.51
Результат: 42.51

Иногда для обяснения решения используют термин «коэффициент», это когда исходную цифру, от которой ищут процент, сначала делят на 100. Получая тем самым коэффициент, соответствующий одному проценту от этой исходной цифры. 327 / 100 = 3.27. После чего умножают этот коэффициент на искомое количество процентов: 3.27 x 13 % = 42.51

От числа 2800 определить 20 %

Итог — 560

Как вычислять: давайте составим пропорцию —
2800 так относится к 100 % как ИКС относится к 20 %
Чтобы определить ИКС нужно умножить 2800 на 20 и разделить на 100. В результате получаем 560.

Как вычислить 24 процента от 650

Давайте воспользуемся коэффициентом, получающимся от деления исходной цифры на 100. То есть 650 разделим на 100. Тем самым мы определим чему равен ОДИН процент от 650. Получается 650 / 100 = 6.5. Один процент от 650 это 6.5, а раз в задании сказано определить 24 %, то нам остаётся только получившийся коэффициент умножить на 24. Результат: 6.5 x 24 = 156.

Лёгкий способ определения процента от числа

При внимательно рассмотрении схемы определения процента от числа видно, что это уравнение, в котором в знаменателе всегда стоит цифра 100. Например, для определения 8 % от 271 нужно решить уравнение: 271 x 8 / 100. А в числителе — искомый процент (в нашем примере цифра 8). Значит можно сначала получить коэффициент 8 / 100 = 0.08, а потом умножить его на первоначальную цифру.

Почему эта схема удобна? Потому, что деление на 100 можно делать в уме! И на калькуляторе исходную цифру от которой ищется процент умножать сразу на него. Вот так: 271 x 0.08 = 21.68

А как легко в уме делить на 100 ? Спросите вы. Очень просто — переносим на два знака влево воображаемую десятичную точку (запятую):
было 8 стало 0. 08
было 45 стало 0.45
было 18 стало 0.18
и так далее.

Успешных вам расчётов и вычислений!

Как посчитать проценты в Excel

Мы сталкиваемся с процентами не только на работе или учебе, но и в нашей повседневной жизни – скидки, чаевые, депозитные ставки, кредиты и прочее. Поэтому умение работать с процентами будет полезно в разных сферах жизни. В этой статье мы ближе познакомимся с процентами, и рассмотрим, как быстро посчитать проценты в Excel, а также на примерах разберем следующие вопросы:

• как посчитать проценты в Excel формула;
• как посчитать процент от числа в Excel;
• как посчитать проценты от суммы в Excel;
• посчитать разницу в процентах Excel;

Как посчитать проценты в Excel формула

Прежде чем перейти к вопросу подсчета процентов в Excel, давайте вспомним основные знания о процентах. Процент – это сотая часть единицы. Из школьной программы вы наверняка знаете, что для того чтобы посчитать проценты, необходимо разделить искомую часть на целое и умножить на 100. Таким образом формула расчёта процентов выглядит следующим образом:

Посчитать проценты в Excel намного проще, так как вычисление некоторых математических операций в Excel происходит автоматически. Поэтому формула расчета процентов в Excel преобразуется следующим образом:

Для того чтобы посчитать проценты в Excel нет необходимости умножать результат на 100, если для ячейки используется Процентный формат.

Рассмотрим наглядный пример, как посчитать процент выполнения плана в Excel. Пусть у нас есть таблица с данными о запланированном объеме реализации продукции и фактическом объеме.

Как посчитать проценты в Excel – Исходные данные для расчета процентов

Для того чтобы посчитать процент выполнения плана необходимо:

• В ячейке D2 ввести формулу =C2/B2 и скопировать ее в остальные ячейки с помощью маркера заполнения.
• На вкладке «Главная» в группе «Число» выбрать «Процентный формат» для отображения результатов в формате процентов.

В результате мы получаем значения, округленные до целых чисел, которые показывают процент выполнения плана:

Как посчитать проценты в Excel – Процент выполнения плана

Следует отметить, что универсальной формулы, как посчитать проценты нет. Все зависит от того, что вы хотите получить в результате. Поэтому в этой статье мы рассмотрим примеры формул вычисления процента от числа, от общей суммы, прироста в процентах и многое другое.

Как посчитать процент от числа в Excel

Для того, чтобы посчитать процент от числа, необходимо использовать следующую формулу:

Рассмотрим пример расчета процента от числа. У нас есть таблица со стоимостью товаров без НДС и ставкой НДС для каждого товара.

Как посчитать проценты в Excel – Исходные данные для расчета процента от числа

Примечание: если вы вручную вводите в ячейке числовое значение и после него ставите знак %, то Excel применяет к данной ячейке процентный формат и воспринимает это число как его сотую часть. Например, если в ячейку ввести 18%, то для расчётов Excel будет использовать значение 0,18.

Пусть нам необходимо рассчитать НДС и стоимость продуктов с налогом на добавленную стоимость.

• Для того чтобы посчитать НДС в денежном эквиваленте, т.е. посчитать процент от числа в ячейке D2 вводим формулу =B2*C2 и заполняем остальные ячейки.
• В ячейке E2 суммируем ячейки B2 и D2, для того чтобы получить стоимость с НДС.

В результате получаем следующие данные расчета процента от числа:

Как посчитать проценты в Excel – Процент от числа в Excel

Как посчитать проценты от суммы в Excel

Рассмотрим пример, когда нам необходимо посчитать проценты от суммы по каждой позиции. Пусть у нас есть таблица продаж некоторых видов продуктов с итоговой суммой. Нам необходимо посчитать проценты от суммы по каждому виду товара, то есть посчитать в процентном соотношении сколько выручки приносит каждый товар от общей суммы.

Как посчитать проценты в Excel – Исходные данные для расчета процентов от суммы

Для этого проделываем следующее:

• В ячейке C2 вводим следующую формулу: =B2/$B$9. Для ячейки B9 мы используем абсолютную ссылку (со знаками $), чтобы она была неизменной, а для ячейки B2 – относительную, чтобы она изменялась при копировании формулы в другие ячейки.
• Используя маркер заполнения копируем эту формулу расчета процентов от суммы для всех значений.
• Для отображения результатов в формате процентов, на вкладке «Главная» в группе «Число», задаем «Процентный формат» с двумя знаками после запятой.

В результате мы получаем следующие значения процентов от суммы:

Как посчитать проценты в Excel – Проценты от суммы в Excel

Посчитать разницу в процентах Excel

Для того чтобы посчитать разницу в процентах, необходимо использовать следующую формулу:

где А – старое значение, а B – новое.

Рассмотрим пример, как посчитать разницу в процентах. Пусть у нас есть данные о продажах за два года. Нам необходимо определить процентное изменение продаж в отчетном году, по сравнению с предыдущим.

Как посчитать проценты в Excel – Исходные данные для расчета разницы в процентах

Итак приступим к расчетам процентов:

• В ячейке D2 вводим формулу =(C2-B2)/B2.
• Копируем формулу в остальные ячейки, используя маркер заполнения.
• Применяем процентный формат для результирующих ячеек.

В результате у нас получается следующая таблица:

Как посчитать проценты в Excel – Вычисление разницы в процентах

В нашем примере положительные данные показывают прирост в процентах, а отрицательные значения – уменьшение в процентах.

Теперь вы знаете, как посчитать проценты в Excel, например, как посчитать процент от числа, проценты от общей суммы и прирост в процентах.

считаем проценты

 Математическая онлайн игра-тренажёр поможет Вам научиться считать проценты для чисел от 10 до 1000

Чтобы отключить звук, нажмите на значок «Динамик» в левом нижнем углы игры.

   1% — это сотая часть числа.

Разделив число на 100, мы как раз и получаем один процент.

Чтобы найти проценты от какого-либо числа надо это число разделить на 100 и результат деления умножить на количество процентов.

Например, чтобы найти 30% от 250, надо 250 поделить на сто (получим 2,5) и потом 2,5 умножить на 30. В результате получится 75. Таким образом, 30% от 250 = 75.

Такой способ подходит для расчётов в уме.

 

Многие проценты можно посчитать проще.

 

10% — это десятая часть числа. Значит, чтобы найти десять процентов от числа, надо это число разделить на 10.

20% — это пятая часть числа. Чтобы вычислить двадцать процентов от числа, его надо разделить на 5.

25% — одна четвёртая или четверть числа. Чтобы вычислить двадцать пять процентов от числа, его надо разделить на 4.

50% — половина. Если разделить число на 2, то как раз и получим пятьдесят процентов от него.

Как просто искать 75 и 80 процентов предлагаю Вам придумать самостоятельно.

 

Решение процентов на калькуляторе

 

На калькуляторе проценты можно считать двумя простыми способами.

С помощью десятичных дробей.

Чтобы найти X% от числа A, мы число A умножаем на X делённое на 100.

То есть, вычисляя 37% от 98, мы 98 умножаем на 0,37.

Или вычисляя 128% от 65, мы 65 умножаем на 1,28.

Используя специальную кнопку %.

На разных моделях калькуляторов работа этой кнопки немного отличается, поэтому разберитесь с этим вопросом самостоятельно.

 

Правила игры

 

В игре представлены задачи на вычисление процентов. Выберите правильный ответ и перетащите его мышкой в мигающую область. Перетаскивать шарик нужно удерживая левую кнопку мышки. За каждый правильный ответ Вы будете получать один балл. За неправильный – обнуляются все баллы.

 

Калькулятор онлайн — Найти число зная его процент

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

Понятие о проценте

Проценты — одно из понятий прикладной математики, которые часто встречаются в повседневной жизни. Так, часто можно прочитать или услышать, что, например, в выборах приняли участие 56,3% избирателей, рейтинг победителя конкурса равен 74%, промышленное производство увеличилось на 3,2%, банк начисляет 8% годовых, молоко содержит 1,5% жира, ткань содержит 100% хлопка и т.д. Ясно, что понимание такой информации необходимо в современном обществе.

Одним процентом от любой величины — денежной суммы, числа учащихся школы и т. д. — называется одна сотая ее часть. Обозначается процент знаком %, Таким образом,
1% — это 0,01, или \( \frac{1}{100} \) часть величины

Приведем примеры:
— 1% от минимальной заработной платы 2300 р. (сентябрь 2007 г.) — это 2300/100 = 23 рубля;
— 1% от населения России, равного примерно 145 млн. человек (2007 г.), — это 1,45 млн. человек;
— 3%-я концентрация раствора соли — это 3 г соли в 100 г раствора (напомним, что концентрация раствора — это часть, которую составляет масса растворенного вещества от массы всего раствора).

Понятно, что вся рассматриваемая величина составляет 100 сотых, или 100% от самой себя. Поэтому, например, надпись на этикетке «хлопок 100%» означает, что ткань состоит из чистого хлопка, а стопроцентная успеваемость означает, что в классе нет неуспевающих учеников.

Слово «процент» происходит от латинского pro centum, означающего «от сотни» или «на 100». Это словосочетание можно встретить и в современной речи. Например, говорят: «Из каждых 100 участников лотереи 7 участников получили призы». Если понимать это выражение буквально, то это утверждение, разумеется, неверно: ясно, что можно выбрать 100 человек, участвующих в лотерее и не получивших призы. В действительности точный смысл этого выражения состоит в том, что призы получили 7% участников лотереи, и именно такое понимание соответствует происхождению слова «процент»: 7% — это 7 из 100, 7 человек из 100 человек.

Знак «%» получил распространение в конце XVII века. В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» Матье де ла Порта. В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращенно от cento). Однако наборщик принял это «с/о» за дробь и напечатал «%». Так из-за опечатки этот знак вошел в обиход.

Любое число процентов можно записать в виде десятичной дроби, выражающей часть величины.

Чтобы выразить проценты числом, нужно количество процентов разделить на 100. Например:

\( 58\% = \frac{58}{100} = 0,58; \;\;\; 4,5\% = \frac{4,5}{100} = 0,045; \;\;\; 200\% = \frac{200}{100} = 2 \)

Для обратного перехода выполняется обратное действие. Таким образом, чтобы выразить число в процентах, надо его умножить на 100:

\( 0,58 = (0,58 \cdot 100)\% = 58\% \) \( 0,045 = (0,045 \cdot 100)\% = 4,5\% \)

В практической жизни полезно понимать связь между простейшими значениями процентов и соответствующими дробями: половина — 50%, четверть — 25%, три четверти — 75%, пятая часть — 20%, три пятых — 60% и т.д.

Полезно также понимать разные формы выражения одного и того же изменения величины, сформулированные без процентов и с помощью процентов. Например, в сообщениях «Минимальная заработная плата повышена с февраля на 50%» и «Минимальная заработная плата повышена с февраля в 1,5 раз» говорится об одном и том же. Точно так же увеличить в 2 раза — это значит увеличить на 100%, увеличить в 3 раза — это значит увеличить на 200%, уменьшить в 2 раза — это значит уменьшить на 50%.

Аналогично
— увеличить на 300% — это значит увеличить в 4 раза,
— уменьшить на 80% — это значит уменьшить в 5 раз.

Задачи на проценты

Поскольку проценты можно выразить дробями, то задачи на проценты являются, по существу, теми же задачами на дроби. В простейших задачах на проценты некоторая величина а принимается за 100% («целое»), а ее часть b выражается числом p%.

В зависимости от того, что неизвестно — а, b или р, выделяются три типа задач на проценты. Эти задачи решаются так же, как и соответствующие задачи на дроби, но перед их решением число р% выражается дробью.

1. Нахождение процента от числа.
Чтобы найти \( \frac{p}{100} \) от a, надо a умножить на \( \frac{p}{100} \):

\( b = a \cdot \frac{p}{100} \)

Итак, чтобы найти р% от числа, надо это число умножить на дробь \( \frac{p}{100} \). Например, 20% от 45 кг равны 45 • 0,2 = 9 кг, а 118% от х равны 1,18x

2. Нахождение числа по его проценту.
Чтобы найти число по его части b, выраженной дробью \( \frac{p}{100} , \; (p \neq 0) \), надо b разделить на \( \frac{p}{100} \):
\( a = b : \frac{p}{100} \)

Таким образом, чтобы найти число по его части, составляющей р% этого числа, надо эту часть разделить на \( \frac{p}{100} \). Например, если 8% длины отрезка составляют 2,4 см, то длина всего отрезка равна 2,4:0,08 = 240:8 = 30 см.

3. Нахождение процентного отношения двух чисел.
Чтобы найти, сколько процентов число b составляет от а \( (a \neq 0) \), надо сначала узнать, какую часть b составляет от а, а затем эту часть выразить в процентах:

\( p = \frac{b}{a} \cdot 100\% \) Значит, чтобы узнать, сколько процентов первое число составляет от второго, надо первое число разделить на второе и результат умножить на 100.
Например, 9 г соли в растворе массой 180 г составляют \( \frac{9 \cdot 100}{180} = 5\% \) раствора.

Частное двух чисел, выраженное в процентах, называется процентным отношением этих чисел. Поэтому последнее правило называют правилом нахождения процентного отношения двух чисел.

Нетрудно заметить, что формулы

\( b = a \cdot \frac{p}{100}, \;\; a = b : \frac{p}{100}, \;\; p = \frac{b}{a} \cdot 100\% \;\; (a,b,p \neq 0 ) \) взаимосвязаны, а именно, две последние формулы получаются из первой, если выразить из нее значения a и p. Поэтому первую формулу считают основной и называют формулой процентов. Формула процентов объединяет все три типа задач на дроби, и, при желании, можно ею пользоваться, чтобы найти любую из неизвестных величин a, b и p.

Составные задачи на проценты решаются аналогично задачам на дроби.

Простой процентный рост

Когда человек не вносит своевременную плату за квартиру, на него налагается штраф, который называется «пеня» (от латинского роеnа — наказание). Так, если пеня составляет 0,1% от суммы квартплаты за каждый день просрочки, то, например, за 19 дней просрочки сумма составит 1,9% от суммы квартплаты. Поэтому вместе, скажем, с 1000 р. квартплаты человек должен будет внести пеню 1000 • 0,019 = 19 р., а всего 1019 р.

Ясно, что в разных городах и у разных людей квартплата, размер пени и время просрочки разные. Поэтому имеет смысл составить общую формулу квартплаты для неаккуратных плательщиков, применимую при любых обстоятельствах.

Пусть S — ежемесячная квартплата, пеня составляет р% квартплаты за каждый день просрочки, а n — число просроченных дней. Сумму, которую должен заплатить человек после n дней просрочки, обозначим S_n.
Тогда за n дней просрочки пеня составит рn% от S, или \( \frac{pn}{100}S \), а всего придется заплатить \( S + \frac{pn}{100}S = \left( 1+ \frac{pn}{100} \right) S \)
Таким образом:
\( S_n = \left( 1+ \frac{pn}{100} \right) S \)

Эта формула описывает многие конкретные ситуации и имеет специальное название: формула простого процентного роста.

Аналогичная формула получится, если некоторая величина уменьшается за данный период времени на определенное число процентов. Как и выше, нетрудно убедиться, что в этом случае
\( S_n = \left( 1- \frac{pn}{100} \right) S \)

Эта формула также называется формулой простого процентного роста, хотя заданная величина в действительности убывает. Рост в этом случае «отрицательный».

Сложный процентный рост

В банках России для некоторых видов вкладов (так называемых срочных вкладов, которые нельзя взять раньше, чем через определенный договором срок, например, через год) принята следующая система выплаты доходов: за первый год нахождения внесенной суммы на счете доход составляет, например, 10% от нее. В конце года вкладчик может забрать из банка вложенные деньги и заработанный доход - «проценты», как его обычно называют.

Если же вкладчик этого не сделал, то проценты присоединяются к начальному вкладу (капитализируются), и поэтому в конце следующего года 10% начисляются банком уже на новую, увеличенную сумму. Иначе говоря, при такой системе начисляются «проценты на проценты», или, как их обычно называют, сложные проценты.

Подсчитаем, сколько денег получит вкладчик через 3 года, если он положил на срочный счет в банк 1000 р. и ни разу в течение трех лет не будет брать деньги со счета.

10% от 1000 р. составляют 0,1 • 1000 = 100 р., следовательно, через год на его счете будет
1000 + 100 = 1100 (р.)

10% от новой суммы 1100 р. составляют 0,1 • 1100 = 110 р., следовательно, через 2 года на его счете будет
1100 + 110 = 1210 (р.)

10% от новой суммы 1210 р. составляют 0,1 • 1210 = 121 р., следовательно, через 3 года на его счете будет
1210 + 121 = 1331 (р.)

Нетрудно представить себе, сколько при таком непосредственном, «лобовом» подсчете понадобилось бы времени для нахождения суммы вклада через 20 лет. Между тем подсчет можно вести значительно проще.

А именно, через год начальная сумма увеличится на 10%, то есть составит 110% от начальной, или, другими словами, увеличится в 1,1 раза. В следующем году новая, уже увеличенная сумма тоже увеличится на те же 10%. Следовательно, через 2 года начальная сумма увеличится в 1,1 • 1,1 = 1,1² раз.

Еще через один год и эта сумма увеличится в 1,1 раза, так что начальная сумма увеличится в 1,1 • 1,1² = 1,1³ раз. При таком способе рассуждений получаем решение нашей задачи значительно более простое: 1,1³ • 1000 = 1,331 • 1000 — 1331 (р.)

Решим теперь эту задачу в общем виде. Пусть банк начисляет доход в размере р% годовых, внесенная сумма равна S р., а сумма, которая будет на счете через n лет, равна S_n р.

Величина p% от S составляет \( \frac{p}{100}S \) р., и через год на счете окажется сумма
\( S_1 = S+ \frac{p}{100}S = \left( 1+ \frac{p}{100} \right)S \)
то есть начальная сумма увеличится в \( 1+ \frac{p}{100} \) раз.

За следующий год сумма S₁ увеличится во столько же раз, и поэтому через два года на счете будет сумма
\( S_2 = \left( 1+ \frac{p}{100} \right)S_1 = \left( 1+ \frac{p}{100} \right) \left( 1+ \frac{p}{100} \right)S = \left( 1+ \frac{p}{100} \right)^2 S \)

Аналогично \( S_3 = \left( 1+ \frac{p}{100} \right)^3 S \) и т.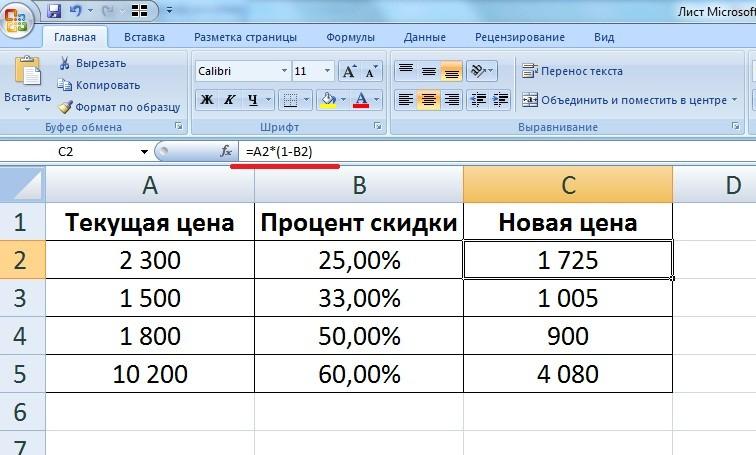 n S \)

Эту формулу называют формулой сложного процентного роста, или просто формулой сложных процентов.

Процент от числа, процентная ставка, Kруговая диаграмма

Часто выполняемыие расчеты с процентами.



	Действия с процентами	Ответ:
1	Число увеличитьуменьшить на процентов (-а)
2	Сколько процентов составляет от числа
3	Какая будет сумма, если составляет процентов (-а)
4	Сколько будет процентов (-а) от
5	Сколько процентов число больше числа
6	Kак % процент перевести в число
7	Число увеличитьуменьшить на Сколько процентов полученное число составляет от начального числа?
8	Отобразить значения в процентах (1-100%) % на круговой диаграмме

процентная ставка. Кредитный калькулятор

 ]]]]]]>]]]]>]]>]]]]]]>]]]]>]]>

Другие полезные темы:

Формулы площади круга, длина окружности круг, длина, окружность, радиус, сегмент, сектор

Площадь круга, длина окружности, площадь сектора, сегмента, длины дуги

Игра Угадай цифру онлайн. Играть бесплатно. Случайные события



Делимся

знаниями

Если думаешь, что Это интересно для друга, напиши

Имя
Комментарий

Вычислить процент чисел

Вычислить процент одного числа от второго числа

Пример расчета процентов по ипотечному кредиту

: у вас есть выплата по ипотеке в размере 800 долларов. У вас есть только 600 долларов, чтобы заплатить банку. Какой процент от общей суммы денег у вас есть? Решение: 600 разделить на 800 равно 0.75. Затем умножьте на 100. Результат равен 75%. Это означает, что вы можете заплатить банку только 75% от общей суммы платежа по ипотеке, и вам потребуется небольшой кредит в размере 200 долларов.

Процентное решение формулы, объясненное с использованием простого соотношения и примера определения того, какой процент равен 2 из 10.
A: B = C: D, поэтому 2 равно 10, как x равно 100.
2/10 = x / 100, тогда Крест умножить 10 x = 200
x = 20 или 20%.

Другие калькуляторы

Калькулятор увеличения или уменьшения процентов поможет найти ответы на ваши вопросы расчета процентов.Чтобы вычислить процент от числа, используйте наш калькулятор процента от числа. Например, найдите 5% процентов от 70. Калькулятор процентов даст вам ответ, это 3,5.

процентов увеличение между двумя числами? Проблема решена с помощью функции «Рассчитать процент увеличения». Найдите процент% увеличения с 2 до 10. Ответ — 400%.

Найдите, что процентов представляет собой число из второго числа ? Пример: узнать, какой процент равен 7 из 300. Калькулятор «Рассчитать процент от двух чисел», ответ — 2.33%.

Новинка: рассчитайте увеличение или уменьшение увеличения заработной платы с помощью нашего калькулятора дохода. Калькулятор процента увеличения заработной платы.

процентов от общего числа . Например, всего = 1100, и вам нужно найти процент, равный 100. Используя наш калькулятор процента от общего количества, ответ составляет 9,09%.

GFC и LCM — математический коэффициент и множитель . Калькулятор наибольшего общего множителя GCF может использоваться для вычисления GFC, а калькулятор наименьшего общего множителя — LCM.

Калькулятор квадратного корня . Вместо того, чтобы запоминать квадратные корни, используйте калькулятор квадратного корня из числа и делайте это на лету. Например, каков квадратный корень из 9? Все мы знаем, что это 3. А как насчет квадратного корня из 500? Узнай себя.

Калькулятор процентов ошибок . Быстро рассчитайте процентную ошибку с помощью калькулятора процентов ошибок.

Калькулятор часов и минут . Найдите минуты или часы с помощью наших калькуляторов.First Calculate Hours in Minutes, очень полезно, чтобы узнать, сколько часов в 300 минутах. Калькулятор «Расчет минут в часах» полезен, чтобы узнать, сколько минут в 5 часах? Ответ: 300 из первой математической задачи.

простая математика Математический калькулятор сложения, математический калькулятор вычитания, математический калькулятор умножения и математический калькулятор деления.

Как рассчитать процент чего-либо

Если вы хотите выработать соответствующий совет в ресторане, узнать, какую процентную скидку вы получаете на продукт или определить конкретный процент от числа, необходимо знать как найти процент чего-то всплывает регулярно. Чтобы рассчитать процентные значения, нужно понимать, что на самом деле означает процент. Преобразование между десятичными пропорциями и процентами простое, но оно также позволяет легко оценивать простые проценты и выполнять более сложные вычисления.

TL; DR (слишком долго; не читал)

Найдите процентное соотношение одного числа по отношению к другому по формуле Percentage = (число, которое вы хотите найти в процентах для ÷ всего) × 100. Переместите десятичную точку два разряда справа, чтобы преобразовать десятичное число в процентное, и два разряда слева, чтобы преобразовать процентное значение в десятичное.Чтобы найти процент от числа, преобразуйте процент в десятичное число, а затем умножьте его на исходное число.

Вычисление основных процентов

Процент — это на самом деле число, показывающее, сколько конкретных вещей на сотню (то есть процентов на латыни). Когда вы определяете процентное соотношение одного числа к другому, нужно выполнить два основных шага. Например, если вы набрали 36 баллов из 60 на тесте, какой процент вы получили? Первый шаг — разделить имеющееся у вас число на желаемое в процентах.Итак, в этом случае:

36 ÷ 60 = 0,6

Это доля от общей полученной вами оценки, максимум 1 (для оценки 60 из 60). Другими словами, это сумма, которую вы получили «на одного». Таким образом, за каждую доступную оценку вы получаете 0,6 балла. Процентный балл — это сумма, которую вы получили за сотню. Это означает, что все, что вам нужно сделать, это умножить этот результат на 100, чтобы получить процент:

\ text {Оценка в процентах} = \ text {оценка в процентах} × 100

\ text {Оценка в процентах} = 0.6 × 100 = 60 \%

Итак, результат теста в процентах составляет 60 процентов. Полное правило таково:

\ text {Percentage} = \ frac {\ text {число, которое вы хотите в процентах}} {\ text {total}} × 100

В качестве другого примера, если пять учеников из 15 имеют коричневый цвет глаза, каков процент студентов с карими глазами? Использование правила дает:

\ text {Percentage} = \ frac {5} {15} × 100 = 33,3 \%

Преобразование процентов в десятичные числа и обратно

Для преобразования десятичного числа в процентное умножьте десятичное. на 100.Это означает перемещение десятичной запятой на два разряда вправо. Например, 0,4 в процентах составляет 40 процентов, а 0,99 в процентах — это 99 процентов.

Чтобы преобразовать процентное значение в десятичное, разделите процент на 100. Это означает, что 23 процента равно 0,23, а 50 процентов — 0,5. Вы можете думать об этом как о перемещении десятичной запятой на два разряда влево.

В некоторых случаях процент также легко выразить дробью. Процент — это числитель дроби, знаменатель которой равен 100.Итак, 25 процентов — это действительно 25/100. В таких случаях дробь легко упростить: 25 процентов на самом деле составляет 1/4, а 30 процентов на самом деле 3/10. Это может быть полезно для вычисления определенного процента числа в вашей голове.

Определение определенного процента числа

Если вы хотите сэкономить 25 процентов от всего, что вы зарабатываете, сколько вам нужно извлечь из зарплаты в 160 долларов? Вычислить конкретный процент числа для подобных ситуаций легко. Сначала преобразуйте желаемый процент в дробную или десятичную дробь.Итак, в этом случае

25 \% = 0,25 = \ frac {1} {4}

Затем умножьте десятичную дробь или дробь на число, которое вы хотите получить в процентах. Для зарплаты в 160 долларов:

0,25 × \ 160 долларов = \ 40 долларов

Это можно сделать, чтобы найти проценты от любого числа.

Увеличение или уменьшение в процентах

Чтобы вычислить процентное изменение определенного числа, выполните два шага. Например, представьте, что товар обычно стоит 50 долларов, но сейчас он доступен за 45 долларов. Сначала найдите общее изменение суммы.Сделайте это, вычтя старое значение из нового. В этом примере 45–50 долларов = –5 долларов. Здесь знак минус означает, что цена снизилась. Затем используйте метод, описанный в первом разделе, чтобы определить, какой это процент от исходной цены. В примере:

\ frac {- \ $ 5} {\ $ 50} × 100 = −10 \%

Следовательно, цена снизилась на 10 процентов.

Если бы цена увеличилась с 50 до 55 долларов, первый шаг привел бы к положительному результату (5 долларов) вместо отрицательного.Окончательный расчет тогда дал бы: (5 $ ÷ 50 $) × 100 = 10 процентов, при этом положительный результат показывает рост цены.

Калькулятор процентов | Как рассчитать процент?

Как найти процентное соотношение двух чисел? — Печенье! 🍪

Процентное соотношение — это также способ выразить отношение между двумя числами в виде доли от 100 . Другими словами, процент говорит нам, как одно число соотносится с другим. Если мы знаем, что число A составляет 25% от числа B , мы знаем, что A от до B похоже на 25 равно 100 или, после еще одного преобразования, например, от 1 до 4, т.е.е., A в четыре раза меньше, чем B . Это то, чему учит процентный калькулятор; что такое процент и как найти процентное соотношение двух чисел. Это необходимые и практические знания. Зачем? Допустим, что B представляет собой массу человеческого тела или массу воздуха. Затем, обозначив A как массу воды, мы можем узнать, каков общий процент воды в организме или относительная влажность (используется для расчета точки росы воздуха).

Как найти процент чего-то? Проще всего объяснить, какой процент у файлов cookie.Удивительно, как часто файлы cookie спасают положение, правда? Скажем, у нас есть большой ящик со 100 отделениями (сетка 10 x 10). Каждое отделение составляет сотую часть или 1% всего ящика. Затем мы заполняем этот ящик печеньем таким образом, чтобы в каждом отсеке было ровно , такое же количество печенья .

Сначала давайте начнем с самого простого примера: 100 файлов cookie . Как получить процент от нескольких, скажем, пяти печенек? Это просто: в каждое отделение помещается ровно одно печенье.Итак, один процент от 100 — это один файл cookie , а пять процентов — это пять файлов cookie.

Давайте что-нибудь посложнее и в четыре раза вкуснее: 400 печенья ! Делим их поровну, и в каждом отделении по четыре печенья. Файлы cookie выглядят меньше, но в нашем воображении они такие же, только ящик намного больше! Один процент от 400 — это 4 . Как насчет 15 процентов? Это 15 отсеков по четыре печенья — 60 печенек. Наши животики начинают немного болеть, но это никогда не мешало нам есть больше печенья!

А теперь еще посложнее — 250 печенья .О-о, мы разделили первые 200 печенек, поместив по два в каждое отделение. Теперь у нас осталось 50 печенек, которые нужно распределить равномерно, хммм, это половина печенья в каждой коробке. Как рассчитать процент? Вы правы — на этот раз 1 процент от общего количества 250 файлов cookie составляет 2,5 . Сколько у нас в 15 коробках? 2,5 * 15 равно 37,5.

Итак, для чего нужен процент? Как мы писали ранее, процент — это способ выразить соотношение. Допустим, вы сдаете оценочный экзамен.Если бы мы сказали вам, что вы набрали 123 балла, это бы вам ни о чем не говорило. 123 из чего? Теперь, если мы вам сказали, что вы получили 82% , эта цифра более понятна. Даже если бы мы вам сказали, вы получили 123 из 150; труднее почувствовать, насколько хорошо ты справился. Неделей ранее был еще один экзамен, и вы набрали 195 из 250, или 78%. Хотя сложно сравнить 128 из 150 и 195 из 250, легко сказать, что оценка 82% лучше, чем 78%. Разве знак процента не полезен? В конце концов, — это процент, который считается !

А как насчет десятичных дробей и процентов? Проценты можно легко преобразовать в десятичные числа. Просто разделите процент на 100, и все готово. 15% равно 0,15. Итак, как мы показали ранее, 0,15 из 250 файлов cookie — это тридцать семь с половиной.

Проценты иногда лучше выражают различные величины, чем десятичные дроби в химии или физике. Например, гораздо удобнее сказать, что процентная концентрация определенного вещества составляет 15,7%, чем 18,66 грамма вещества в 118,66 граммах раствора (как в примере в калькуляторе процентной концентрации). Другой пример — эффективность (или ее частный случай — эффективность Карно). Что лучше сказать, что автомобильный двигатель работает с КПД 20% или что он производит выходную энергию 0,2 кВтч из 1 кВтч энергии на входе? Что вы думаете? Мы уверены, что вы уже хорошо знаете, что умение получать процент от числа — это ценная способность.

Поиск процентов — Как найти проценты

Слово процентов означает одну часть из ста.

Процент — это число или отношение в виде дроби от 100. За числом в процентах всегда следует символ процента (%) . Ниже приведены примеры процентов:

`5%, 10%, 33 1/3% ‘, 67,5%, 100%`

Процент применяется в разных областях. Он обычно используется в бухгалтерском учете и финансах, таких как процентные ставки, прибыль, продажи и налогообложение. Ряд школ и университетов использовали проценты для выражения оценок учеников. Вероятности, пищевая ценность и загрузка процесс представлены в процентах.

---

Запоминание

Дробь	соотношение между двумя ненулевыми целыми числами.Ex. 1/2
Коэффициент	соотношение между двумя числами. Ex. 1: 2
Смешанное число	целое число и правильная дробь. Ex. 1 2/3
Правильная фракция	дробь, числитель которой меньше знаменателя. Ex. 3/4
Кол. Акций	число, представляющее сумму или значение
Отличить	идентифицируют различия между двумя или более предметами.

---

Расчет процента

Процент — это результат умножения определенного числа на процент.В большинстве случаев проценты меньше числа, поскольку проценты является частью числа или количества. Но бывают случаи, что процент больше числа. Это произойдет, если процент больше 100%.

Короче говоря, процент — это определенный процент от числа.

В большинстве случаев после количества следует фраза «процент от».

Например;

В этом заявлении 50 — это количество, 35 — это процент и 70% — это процент.

Пример 3:

24

Пояснение:

40 — это проц.

60 — количество.

Процент — это необходимое количество.

Умножение числа на процент;

`60` x` 40% = 60` x `40/100 = 2400/100 = 24`

Следовательно, 40% от 60 равно 24.

Пример 4:

27

Пояснение:

75 — это проц.

36 — количество.

Умножение числа на процент;

`36` x` 75% = 36` x `75/100 = 2700/100 = 27`

Следовательно, 27 составляет 75% от 36.

---

Вычисление процента

При нахождении процента числа разделите процент на количество, а затем умножьте произведение на 100.Поместите символ процента (%) после конечного продукта.

Если процент больше количества, это означает, что процент больше 100%. Процент — это фактор увеличения стоимости количества.

Пример 5:

25%

Пояснение:

18 — это процент.

72 — количество.

Процент спрашивается.

Деление процента на количество;

Умножаем произведение на 100 и ставим символ процента (%) после;

Следовательно, 18 составляет 25% от 72.

Пример 6:

80%

Пояснение:

12 — процент

15 — количество.

Процент спрашивается.

Деление процента на количество;

Умножаем произведение на 100 и ставим символ процента (%) после;

Следовательно, 12 составляет 80% от 15.

, пример 7:

200%

Пояснение:

100 — процент

50 — количество.

Процент спрашивается.

Деление процента на количество;

Умножаем произведение на 100 и ставим символ процента (%) после;

Следовательно, 100 — это 200% от 50.

---

Преобразование процентов в десятичные числа

Для получения процентов необходимо преобразовать процент в десятичную форму, прежде чем умножать их на количество.

Вот шаги для преобразования процентов в десятичные числа:

1. Пренебрегайте символом процента (%).

2. Переместите десятичную запятую на два разряда влево.

Пример 8:

0,1

Пояснение:

Пропустите символ процента (%) и переместите десятичную запятую на 2 позиции влево.

Следовательно, 10% — это 0,1 в десятичной системе.

, пример 9:

0,0531

Пояснение:

Пропустите символ процента (%) и переместите десятичную запятую на 2 позиции влево.

Следовательно, 0,0531 — это десятичная форма 5,31%.

Пример 10:

4,28

Пояснение:

Пропустите символ процента (%) и переместите десятичную запятую на 2 позиции влево.

Следовательно, 4,28 — это десятичная форма 428%.

---

Преобразование десятичной дроби в проценты

Преобразовать десятичные числа в проценты легко: просто переместите десятичную запятую на два разряда вправо, а затем поместите символ процента (%) после.

Пример 11:

60.7%

Пояснение:

Переместите десятичную запятую на 2 разряда вправо и поместите символ процента (%) после нее.

Следовательно, 0,607 — это 60,7%.

, пример 12:

120.8%

Пояснение:

Переместите десятичную запятую на 2 разряда вправо и поместите символ процента (%) после нее.

Следовательно, 1,208 составляет 120,8%.

---

Преобразование процента в дробь

Иногда более простой способ получить процентное значение — преобразование процента в дробь.Дроби предпочтительнее использовать, чем десятичные, если десятичная дробь имеет много цифр. Это делает умножение более удобным, поскольку для упрощения процента используется только факторизация.

Вот шаги по преобразованию процента в дробь:

1. Пренебрегайте символом процента (%).

2. Разделите процент на 100. Если в числителе есть цифры справа от десятичной точки, перемещайте десятичную точку, пока числитель не станет целым числом.Переместите десятичную точку знаменателя (равную 100) на то же количество десятичных знаков, на которое переместилась десятичная точка числителя.

3. Снизьте до самых низких сроков.

Пример 13:

`4/25`

Пояснение:

Пропустите символ процента (%) и разделите процент на 100.

Уменьшить до самых низких сроков.

`16/100 = текст (2 x 2 x 2 x 2) / текст (2 x 2 x 5 x 5) = текст (2 x 2) / текст (5 x 5) = 4/25`

Следовательно, 16% в виде дроби составляет «4/25».

Пример 14:

`5/8`

Пояснение:

Пропустите символ процента (%) и разделите процент на 100.

Переместите десятичную точку в числителе и знаменателе на 1 десятичный знак вправо, чтобы числитель стал целым числом.

Уменьшить до самых низких сроков.

`625/1000 = текст (5 x 5 x 5 x 5) / текст (2 x 2 x 2 x 5 x 5 x 5) = 5 / текст (2 x 2 x 2) = 5/8`

Следовательно, 62.5% в долях: «5/8».

Пример 15:

`8 1 / 25` или` 201 / 25`

Пояснение:

Пропустите символ процента (%) и разделите процент на 100.

Уменьшить до самых низких сроков.

`804/100 = текст (2 x 2 x 201) / текст (2 x 2 x 5 x 5) = 201 / текст (5 x 5) = 201/25 или 6 1/25`

Следовательно, форма дроби для 804% — «8 1/25» или «201/25».

---

Преобразование дроби в проценты

При преобразовании дробей в проценты проще и удобнее сначала преобразовать дробь в десятичную, а затем преобразовать десятичную в проценты.

Вот шаги по преобразованию дробей в проценты:

1. Разделите числитель дроби на знаменатель. Результат в десятичной форме.

2. Умножьте десятичную форму на 100.

3. Поместите символ процента (%) после последней цифры процента.

В случае смешанных номеров;

1. Выполните описанные выше действия только для правильной доли смешанного числа.

2. Умножьте целое число смешанной дроби на 100.

3. Сложите произведение (целое число, умноженное на 100) и десятичную форму правильной дроби.

4. Поместите символ процента (%) после последней цифры процента.

---

Пример 16:

60%

Пояснение:

Разделите числитель на знаменатель.

0,6 5 3,0 0 30 30 0

Умножьте десятичную форму на 100 и поместите символ процента после последней цифры.

Следовательно, «3/5» составляет 60%.

, пример 17:

225%

Пояснение:

Разделите числитель на знаменатель.

`2.25 4 9.00 8 10 8 20 20 0`

Умножьте десятичную форму на 100 и поместите символ процента после последней цифры.

Следовательно, «9/4» составляет 225%.

Пример 18:

112,5%

Пояснение:

Разделите числитель правильной дроби на знаменатель.

`0,125 8 1.000 0 10 8 20 16 40 40 0`

Умножьте десятичную форму на 100.

Умножьте целое число смешанного числа на 100.

Сложите произведение (целое число, умноженное на 100) и десятичную форму правильной дроби.

Следовательно, «1 1/8» составляет 112,5%.

---

Различие процента и процента

Существуют некоторые заблуждения относительно использования слов процента и процента.В двух словах есть

процентов относится к определенному числу.

Например;

Бернадетт правильно ответила на 90 процентов вопросов теста.

Она набрала 90% (процентов) в тесте.

процента — это результат умножения числа на процент. Он обозначает часть и в основном описывается как более низкий или высокий.

Например;

Bernadette получила высокий процент в тесте.

Она набрала в тесте процент 90/100.

Как правило, слово «процент» следует после определенного числа, и обычно это целые или счетные числа. Он обычно не используется в предложениях, так как всегда заменяется символом процента (%). Слово «процент» стоит перед дробью или после прилагательного (напр.г. высокий, низкий, большой, маленький).

---

Примеры процентов

Пример 1:

процентов

Пояснение:

10 — это конкретное число, поэтому используется процент.

Пример 2:

процентов

Пояснение:

Слово «низкий» используется и поэтому используется процент.

---

3 простых способа вычисления процентов (математика)

Как вычислить проценты проще, чем вы думаете. Изучение этого может помочь вам легко рассчитывать чаевые в ресторанах и использовать проценты для простого расчета продажных цен при покупках.

Если вы не знаете, как выполнять какие-либо из этих удобных вычислений, или если вам просто нужно освежить общее процентное соотношение, ознакомьтесь с нашим руководством по вычислению процентов ниже.

СОДЕРЖАНИЕ

1. Расчет процента от целого

Для расчета процента должна быть известна вся сумма. Это в дополнение к процентной или порционной сумме. Вас могут спросить, «какой процент W составляет P», где W — это все количество, а P — количество порций. Или вопрос может заключаться в том, «сколько X процентов от W», где X представляет собой процентную цифру.

1. Что такое процент?

Процент — это способ выразить число как часть целого. Чтобы вычислить процент, мы смотрим на все как на 100%. Например, у вас есть 10 яблок (= 100%). Если вы съели 2 яблока, то вы съели 2/10 × 100% = 20% ваших яблок, и у вас останется 80% ваших исходных яблок.

Термин «процент» в английском языке происходит от итальянского per cento или французского pour cent, что буквально означает «за сотню».

2. Какова стоимость целого?

Например, у нас есть банка, содержащая 1199 красных шариков и 485 синих шариков, что в сумме составляет 1684 шарика.В этом случае 1684 составляет целую банку из шариков и будет установлено равным 100%.

3. Превратите значение в проценты.

Допустим, мы хотим узнать, какой процент емкости занимает 485 синих шариков.

4. Объедините два значения в дробь.

В нашем примере нам нужно выяснить, какой процент 485 (количество синих шариков) составляет 1684 (общее количество шариков). Следовательно, в данном случае дробь равна 485/1684.

5. Преобразуйте дробь в десятичную.

Чтобы преобразовать 485/1684 в десятичную дробь, разделите 485 на 1684. Получается 0,288.

Формула: 485/1684 = 0,288

6. Преобразуйте десятичную дробь в проценты

Умножьте результат, полученный на предыдущем шаге, на 100. В этом примере 0,288, умноженное на 100, равно 28,8 или 28,8%.

Формула: 0,288 x 100 = 28,8 или 28,8%

Простой способ умножить десятичную дробь на 100 — это переместить десятичную дробь на два места вправо.

2. Обратное процентное соотношение

Вы можете столкнуться с вопросом, который попросит вас работать в обратном направлении и найти первоначальную цену чего-либо после того, как цена увеличилась.Если вам дается количество после процентного увеличения или уменьшения, вам может потребоваться найти исходную сумму.

1. Когда делать обратный процент?

Иногда вам задают процент от суммы, и вам нужно знать числовое значение процента. Примеры включают расчет налогов, чаевых и процентов по кредиту.

2. Начальные числа

Допустим, вы заняли деньги у друга, который собирается взимать с вас проценты. Сумма займа изначально составляла 15 долларов, а процентная ставка — 3% в день.Это единственные два числа, которые вам нужны для расчета.

3. Преобразуйте процент в десятичную дробь.

Умножьте процент на 0,01 или просто переместите десятичную дробь на два разряда влево. Это превращает 3% в 0,03.

Формула: 3% x 0,01 = 0,03

4. Умножьте начальную сумму на новое десятичное число.

В этом случае умножьте 15 на 0,03. Это составляет 0,45. В этом примере 0,45 доллара — это сумма процентов, начисляемых каждый день, когда вы не возвращаете своему другу.

Формула: 0.3 x 15 = 0,45 (сумма начисленных процентов)

3. Расчет скидок

Делаете покупки, но хотите сэкономить, выбирая товары со скидкой? Изучение того, как решать процентные ставки скидки, поможет вам понять, действительно ли вы экономите деньги или тратите их зря.

1. Цена и размер скидки

Это очень простой способ рассчитать цену со скидкой, но вы должны начать с точного процента скидки. Дважды проверьте, за что продается ваш товар.

2. Напротив процентов скидки.

Противоположность процента — 100% минус процент, с которым вы работаете. Если вы хотите купить рубашку со скидкой 30%, то наоборот — 70%.

Формула: 100% — 30% (скидка) = 70%

3. Преобразуйте противоположный процент в десятичную дробь.

Чтобы преобразовать процент в десятичное число, умножьте его на 0,01 или переместите десятичный разделитель на два разряда влево. В этом примере 70% становится 0,7.

Формула: 70% x 0,01 = 0,7

4.Умножьте цену на новое десятичное число

Если вам нужна рубашка за 20 долларов, умножьте 20 на 0,7. Получается 14. Это означает, что рубашка продается за 14 долларов.

Формула: 20 долларов (цена товара) x 0,7 = 14 (цена товара со скидкой)

Вы нашли эту статью полезной? Поделитесь этим с вашими друзьями!

Как рассчитать процент от числа

Изучите основы расчета процентов от количества в этом простом уроке! Чтобы найти процентное значение любого числа, используйте этот общий принцип ПЕРЕВОДА: замените процент на десятичное число, а слово «из» на умножение.См. Множество примеров ниже.

Концепции и идеи этого урока также объясняются в этом видео:

Вы узнали, что найти 1% числа означает найти 1/100 числа Это. Точно так же найти 60% числа означает найти 60/100 (или 6/10) его. В этих выражениях слово «из» переводится как умножение: 1% от 90 → 1% × 90 и 60% от 700 долларов → 60% × 700 долларов. Мы также можем записать эти проценты как десятичных знаков : 1% от 90 → 0,01 × 90 60% от 700 долларов → 0,6 × 700 долларов. Это дает нам другой способ вычислить процентное отношение числа (или процент некоторого количества):

Чтобы вычислить процент от некоторого числа, измените процент в десятичной дроби, а слово «из» в умножение.

Пример 1. Найдите 70% от 80. Следуя ярлыку, запишем это как 0,7 × 80. Помните, что в десятичное умножение, вы умножаете, как если бы не было десятичных знаков, и в ответе будет столько десятичных цифр справа от десятичной точки как общее количество десятичных цифр всех множителей. Итак, когда вы умножаете 0,7 × 80, подумайте о умножении 7 × 80 = 560. Поскольку 0,7 имеет одну десятичную цифру, а 80 — нет, В ответе одна десятичная цифра: 56.0 Таким образом, 0,7 × 80 = 56. Вы также можете использовать «здравый смысл», чтобы рассуждать логически: 0,7 × 80 должно быть меньше 80, но больше 1/2 от 80, то есть 40. Поскольку 7 × 8 = 56, вы знаете, что ответ должен быть 56, а не 5,6 или 560.

Пример 2. Найдите 3% от 4000 долларов. Сначала запишите это как 0,03 × 4000 долларов. Затем умножаем 3 × 4000 долларов = 12000 долларов. Наконец, поставьте десятичную точку там, где она дает ответ два. десятичные цифры: 120 долларов.00.

Пример 3. Найти 23% из 5 500 км. Запишите выражение как 0,23 × 5 500 км и используйте калькулятор для расчета продукта. Ответ — 1265 км. Этот ответ заставляет смысл, потому что 10% из 5 500 км составляет 550 км, поэтому 20% — это 1100 км. Таким образом 1265 км как 23% от 5500 км — разумный ответ.

1. «Перевести» выражения в умножение на десятичную дробь.Рассчитайте.

а. 20% от 70 ______ × ______ = ______

г. 90% от 50 ______ × ______ = ______

г. 9% от 3000 ______ × ______ = ______

2. «Перевести» в другую сторону: запишите умножение как выражение «процент от числа».

а. 0,6 × 50 _____% от ______ = ______

г. 0,03 × 400 $ _____% от ______ = ______

г. 0,08 × 6 _____% от ______ = ______

3. Используйте калькулятор, чтобы найти проценты от этих количеств.

а. 17% от 4500 долларов США

г. 67% от 27 м

4.Используйте мысленную математику, чтобы найти их процентное соотношение количества.

5. а. Озеро с береговой линией протяженностью 30 км. 6% от этого Песчаный пляж. Какой процент береговой линии составляет , а не песчаный пляж?

6. Двадцать процентов из 4000 студентов университета имеют стипендия.

а. Что процентов учащихся не стипендия?

г. Сколько студентов получают стипендию?

8. Определите ошибки, которые допустила Глэдис. Тогда найдите правильный ответ.

Найдите 80% из 50.

Решение Глэдис:
80 × 50 = 4 000

9. Найдите выражения с тем же значением, что и 20%. 620 долларов.

0,02 × 620 долл. США	$ 620 ÷ 5
$ 620 ÷ 10 × 2	2 × 62 $
1 5 × 620 долл. США	0.2 × 620 долл. США
20 × 620 долл. США	$ 620 ÷ 4

11. В таблице ниже показано, как Энди использовал время за один день.

а. Подсчитайте время, которое он потратил на каждое занятие.
Округлите минуты до ближайшей минуты.

г. Обозначьте секции на круговой диаграмме значком название каждого вида деятельности.

Использование времени Энди

Деятельность Процент Минуты часов / минут Спящий режим 38% Школа 21% Футбол 10% 144 2 ч 24 мин Играть 11% Питание 9% Работа по дому 9% Гигиена 2% ИТОГО 100% 1440 24 часа

См.

Также

Процент — бесплатное занятие

Процент числа с использованием мысленной математики — бесплатный урок

Как считать проценты — бесплатное занятие

Основы процента изменения — бесплатное занятие

Интерактивный инструмент дроби, десятичной дроби и процента
Этот инструмент показывает дробь визуально (столбик или круговая диаграмма) и преобразует дробь в проценты и десятичные дроби.Вы можете показать или скрыть эквивалентные процентные и десятичные дроби.
/interactives/fraction_decimal_percentage.php

---

Этот урок взят из книги Марии Миллер «Math Mammoth Percent» и размещен на сайте www.HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер.

---

Калькулятор процентов — Расчет процентов

Что такое проценты?

Один процент — сотая.Мы используем% для обозначения этого. Итак, 5 процентов — это то же самое, что 5%, 0,05, 5/100 или пять сотых. Это так просто! Это хорошо, но обычно мы используем не только проценты. Иногда мы хотим показать соотношение между двумя числами. Например: что 40% от 20? Это 40 сотых от 20, так что если мы разделим 20 печенек на 100 равных частей (удачи с этим!), 40 из этих кусочков будут нашими 40% от 20 печений. Давайте посчитаем: 40/100 * 20 = 8. Здесь применима небольшая хитрость: если вы хотите разделить на сотню, просто переместите запятую на два места влево.В нашем расчете 40/100 * 20 мы могли бы сделать так: (40 * 20) / 100 (это то же самое). 40 * 20 равно 800. Переместите запятую на 800 на 2 позиции влево, и вы получите 8.00. Введите эти значения вверху страницы: 40 и 20. Тогда вы получите «40% от 20 равно 8». В другом случае вы хотите указать, например, на сколько процентов уменьшилось или увеличилось число. Например, если у вас есть 10 яблок и вы съели 2 из них … Тогда вы потеряли 20% яблок. Зачем? Поскольку 8 — это 80% от 10. Все яблоки были 100%, теперь у нас все еще есть 80%, поэтому количество яблок уменьшилось на 20% (потому что 100 — 80 = 20).Используйте для этого наш инструмент увеличения процента.

Происхождение

Термин процент происходит от латинского на центр (на сотню) и обозначается знаком%.

Проценты на решения

Процент не всегда означает несколько сотых от целого. Таким образом, решения также отображаются в процентах. К физиологическому солевому раствору, например, относится 0,9% раствор кухонной соли. Это 0,9% означает, что раствор содержит 0.9 грамм соли на 100 мл (= 100 грамм). Таким образом, процент здесь относится к весу. В процентном соотношении объема часто указывается добавление: «об.», Тогда мы получаем, например, 14 об.% Или 14 об.%.

Процентные точки

Процентная точка, также записываемая как%, используется для обозначения абсолютной разницы между значениями, выраженной в процентах. Таким образом, процент — это сотая часть, а процентный пункт — это расчетная единица, которая выражает изменение в процентах.

No related posts.